Артикул: 1165995

Раздел:Технические дисциплины (109492 шт.) >
  Теоретическая механика (теормех, термех) (2302 шт.) >
  Динамика (393 шт.)

Название или условие:
Задача Д1
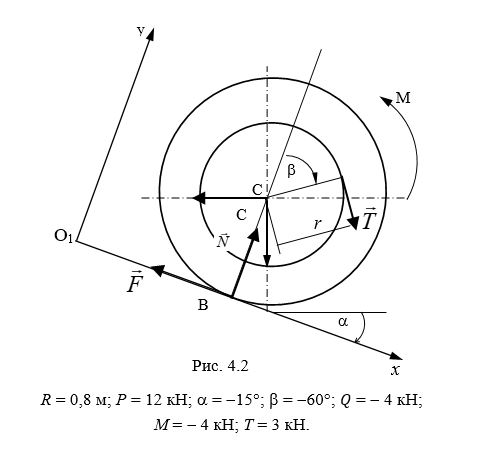
4.1.1. Условия задачи. Барабан радиусом R и весом Р (рис. 4.1), имеющий выточку радиусом r = 0,6R с намотанным на нее тросом, находится в зацеплении с наклонной плоскостью (может катиться по плоскости без проскальзывания). Угол между наклонной плоскостью и горизонталью α. Радиус инерции барабана с тросом ρ = 0,5R.
На барабан помимо силы веса P действуют следующие активные (заданные) нагрузки:
- сила натяжения троса T, действующая по касательной к выточке, точка ее приложения задается углом β, отсчитываемым от нормали к плоскости, как показано на рис. 4.1;
- горизонтальная сила Q, приложена к оси С барабана;
- пара сил с моментом М.
Численные значения характеристик плоскости, барабана и заданных нагрузок для различных вариантов задачи приведены в табл. Д1.
Под действием указанных сил барабан начинает движение из состояния покоя.
Вариант 789

Описание:
Пренебрегая сопротивлением качения, получить закон движения центра масс С барабана как функцию времени. Расчет ускорения центра масс провести двумя способами:
а) используя дифференциальные уравнения плоскопараллельного движения твердого тела;
б) считая движение барабана чистым вращением вокруг мгновенного центра скоростей (мгновенной оси вращения) О.
Определить, возможно ли движение барабана по полученному закону без скольжения, если вместо зацепления между барабаном и плоскостью будет контакт шероховатых поверхностей с коэффициентом трения f = 0,4.

Подробное решение в WORD

Изображение предварительного просмотра:

Процесс покупки очень прост и состоит всего из пары действий:
1. После нажатия кнопки «Купить» вы перейдете на сайт платежной системы, где можете выбрать наиболее удобный для вас способ оплаты (банковские карты, электронные деньги, с баланса мобильного телефона, через банкоматы, терминалы, в салонах сотовой связи и множество других способов)
2. После успешной оплаты нажмите ссылку «Вернуться в магазин» и вы снова окажетесь на странице описания задачи, где вместо зеленой кнопки «Купить» будет синяя кнопка «Скачать»
3. Если вы оплатили, но по каким-то причинам не смогли скачать заказ (например, случайно закрылось окно), то просто сообщите нам на почту или в чате артикул задачи, способ и время оплаты и мы отправим вам файл.
Условия доставки:
Получение файла осуществляется самостоятельно по ссылке, которая генерируется после оплаты. В случае технических сбоев или ошибок можно обратиться к администраторам в чате или на электронную почту и файл будет вам отправлен.
Условия отказа от заказа:
Отказаться возможно в случае несоответсвия полученного файла его описанию на странице заказа.
Возврат денежных средств осуществляется администраторами сайта по заявке в чате или на электронной почте в течении суток.

Похожие задания:

Определить скорость V3	Динамика точки. Вариант 8 На тело массой m, движущееся по горизонтальной гладкой поверхности вдоль оси x, действует сила, проекция которой равна Fx = −0,5x. В начальный момент x0 = 0, v0x = 10 м⁄с. Определить максимальное значение координаты x тела
Найдите ускорение тела (1)	Задание Д4. Исследование относительного движения материальной точки Шарик М, рассматриваемый как материальная точка, перемещается по цилиндрическому каналу движущегося тела А (рис. 11). Найти уравнение относительного движения этого шарика х = f(t), приняв за начало отсчета точку О. Тело А равномерно вращается вокруг неподвижной оси (ось вращения z1 вертикальна). Найти также координату х и давление шарика на стенку канала при заданном значении t = t1. Вариант 7 Дано: m = 0,03 кг; ω = 2π рад/с; х0 = 0,3 м; ; t1 = 0,2 с; h = 0,2 м; f = 0.
Задание Д6 Шарик, принимаемый за материальную точку, движется из положения А внутри трубки, ось которой расположена в вертикальной плоскости (рис. 1). Найти скорость шарика в положениях B и C и давление шарика на стенку трубки в положении C. Трением на криволинейных участках траектории пренебречь. Вариант 7 Дано: m = 0,4 кг; VА = 5 м/с; τ = 5 с; R = 1,0 м; f = 0,10; α = 30°; h0 = 5 см; с = 5 Н/см.	Лыжник массой m = 70 кг опускается без начальной скорости по склону, составляющему угол α = 30° с горизонтом, не отталкиваясь палками. Длина спуска l = 100 м, коэффициент трения скольжения лыж о снег f = 0.1. Сила сопротивления воздуха пропорциональна квадрату скорости R = 0.4v2. Определить скорость лыжника в конце спуска.
Задача 3.1 Груз массой m, получив в точке А начальную скорость V0, движется по гладкой горизонтальной поверхности под действием постоянной силы Q. На груз действует сила сопротивления R, зависящая от скорости груза. Определить скорость груза в момент времени t1. Вариант 5 Дано: R=µ*V=0.4*V(H), m=4кг, V0=20м/с, µ=0.4H*c/м, t1=5c, g≈9.81м/c2, Q=4H. Определить: V1-?	Задача Д1 Динамика точки Твердое тело, размерами которого в данной задаче можно пренебречь, движется из точки А по участку АВ (длиной l) по наклонной поверхности, составляющей угол α с горизонтом, в течение τ секунд. Его начальная скорость VA. Коэффициент трения скольжения тела по плоскости равен f. В точке В тело покидает плоскость со скоростью VB и попадает со скоростью VB в точку С плоскости BD, наклоненной под углом β к горизонту, находясь в воздухе Т секунд. Сопротивление воздуха не учитывать. Вариант 1 Дано: α = 30°; VA= 1 м/с ; f = 0.3; l=10 м; β= 60°; Определить время τ и высоту h
Задание Д1. Интегрирование дифференциальных уравнений движения материальной точки, находящейся под действием постоянных сил Лыжник подходит к точке А участка трамплина АВ, наклоненного под углом α к горизонту и имеющего длину l (рис. 9), со скоростью vA. Коэффициент трения скольжения лыж на участке АВ равен f. Лыжник от А до В движется τ с; в точке В со скоростью vB он покидает трамплин. Через Т с лыжник приземляется со скоростью vC в точке С горы, составляющей угол β с горизонтом. При решении задачи принять лыжника за материальную точку и не учитывать сопротивление воздуха. Вариант 7 Числовые данные: α = 15°; f = 0,1; vA = 16 м/с; l = 5 м; β = 45°. Определить vВ и Т.	Задание Д9. Применение теоремы об изменении кинетического момента к определению угловой скорости твердого тела Тело Н массой m1 вращается вокруг вертикальной оси z с постоянной угловой скоростью ω0; при этом в точке О желоба АВ тела Н на расстоянии АО от точки А, отсчитываемом вдоль желоба, находится материальная точка К массой m2. В некоторый момент времени (t = 0) на систему начинает действовать пара сил с моментом Mz = Mz(t). При t = τ действие сил прекращается. Определить угловую скорость ωτ тела Н в момент t = τ. Тело Н вращается по инерции с угловой скоростью ωτ. В некоторый момент времени t1 = 0 (t1 - новое начало отсчета времени) точка К (самоходный механизм) начинает относительное движение из точки О вдоль желоба АВ (в направлении к В) по закону OK = s = s (t1). Определить угловую скорость ωТ тела Н при t1 = Т. Тело Н рассматривать как однородную пластинку, имеющую форму, показанную на рисунке. Вариант 7 Дано: m1 = 300 кг; m2 = 50 кг; ω = - 2 рад/с; а = 1,6 м; b = 1 м; R = 0,8 м; АО = 0; Mz=Mz*=968 Нм ; τ = 1 с; OK=s =(πR/2)·t12 ; Т = 1 с.