Артикул: 1167016

Раздел:Технические дисциплины (110513 шт.) >
  Теоретическая механика (теормех, термех) (2372 шт.) >
  Динамика (407 шт.)

Название или условие:
Курсовая работа по теоретической механике
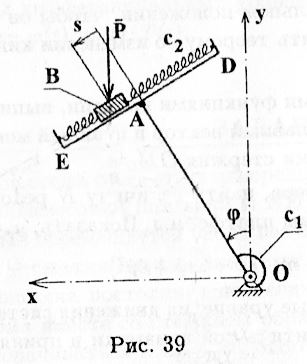
ЗАДАНИЕ 39
Система состоит из однородного стержня OA длины l и массы m1 и невесомой платформы ED, несущей ползун B массы m2, который перемещается вдоль нее без трения под действием растяжения-сжатия двух одинаковых пружин жесткости с2. К ползуну приложена постоянная по величине вертикальная сила P. Платформа вместе со стержнем образует твердое тело, которое может поворачиваться вокруг опорного шарнира, имеющего спиральную пружину жесткости c1 (рис. 39).

Описание:
1. Ввести подвижную систему координат, связанную со стержнем ОА. Считая φ(t) и s(t) заданными функциями времени, вычислить абсолютную скорость и абсолютное ускорение ползуна А. Изобразить на чертеже составляющие Vабс и ωабс.
2. Считая φ(t) заданной функцией времени, составить дифференциальное уравнение движения ползуна А относительно подвижной системы координат, введенной в п. 1.
3. Считая функции φ(t) и s(t) известными, найти проекции Rx и Ry реакции шарнира О. Воспользоваться теоремой об изменении количества движения. Показать, что
Rx=[(m1/2)+m2 ]l(φ ̈ cos⁡φ-(φ² sin⁡φ ) ̇ )+m2 [(s ̈-s(φ² ) ̇ ) cos⁡φ-(2s ̇φ ̇+sφ ̈ ) sin⁡φ ];
Ry=-[(m1/2)+m2 ]l(φ ̈ sin⁡φ+(φ² ) ̇ cos⁡φ )-m2 [(s ̈-s(φ² ) ̇ ) sin⁡φ+(2s ̇φ ̇+sφ ̈ ) cos⁡φ ]+(m1+m2 )g+P.
4. Полагая, что ползун закреплен в точке А и P = 0, помощью теоремы об изменении кинетического момента составить дифференциальное уравнение вращательного движения системы.
5. Для условия п. 4 найти угловую скорость ω0, которую надо сообщить стержню в вертикальном положении, чтобы он смог отклониться на угол φ_0. Применить теорему об изменении кинетической энергии.
6. Считая φ(t) и s(t) заданными функциями времени, выписать силы инерции ползуна, а также главный вектор и главный момент относительно точки О сил инерции стержня ОА.
7. Применяя принцип Даламбера, найти величину N реакции, действующей на ползун со стороны платформы. Показать, что

N=(P+m_2 g)cos⁡φ-m2(sφ ̈+2s ̇φ ̇+lφ ̇^2)

8. Составить дифференциальные уравнения движения системы, исходя из общего уравнения аналитической динамики и приняв за обобщенные координаты φ и s.
9. Составить выражения для кинетической и потенциальной энергии системы, вычислить обобщенные силы.
10. Используя уравнения Лагранжа второго рода, показать, что дифференциальные уравнения движения системы имеют вид
(m1/3) l² φ ̈+m2 [2ss ̇φ ̇+(l²+s² ) φ ̈+ls ̈ ]=(m1/2)gl sin⁡φ+(P+m2 g)(l sin⁡φ+s cos⁡φ )-c1φ;
m2 (s ̈+lφ ̈-s(φ² ) ̇ )=(P+m2 g) sin⁡φ-2c2s.
11. Для условия п. 4 определить интервал жесткости спиральной пружины, для которого верхнее вертикальное положение равновесия системы будет устойчивым. Составить уравнение малых колебаний системы в окрестности устойчивого положения равновесия, найти период малых колебаний.

Подробное решение - скан рукописи

Изображение предварительного просмотра:

Процесс покупки очень прост и состоит всего из пары действий:
1. После нажатия кнопки «Купить» вы перейдете на сайт платежной системы, где можете выбрать наиболее удобный для вас способ оплаты (банковские карты, электронные деньги, с баланса мобильного телефона, через банкоматы, терминалы, в салонах сотовой связи и множество других способов)
2. После успешной оплаты нажмите ссылку «Вернуться в магазин» и вы снова окажетесь на странице описания задачи, где вместо зеленой кнопки «Купить» будет синяя кнопка «Скачать»
3. Если вы оплатили, но по каким-то причинам не смогли скачать заказ (например, случайно закрылось окно), то просто сообщите нам на почту или в чате артикул задачи, способ и время оплаты и мы отправим вам файл.
Условия доставки:
Получение файла осуществляется самостоятельно по ссылке, которая генерируется после оплаты. В случае технических сбоев или ошибок можно обратиться к администраторам в чате или на электронную почту и файл будет вам отправлен.
Условия отказа от заказа:
Отказаться возможно в случае несоответсвия полученного файла его описанию на странице заказа.
Возврат денежных средств осуществляется администраторами сайта по заявке в чате или на электронной почте в течении суток.

Похожие задания:

Задача Д1 Груз D массой m=6кг, получив в точке А начальную скорость V0=15м/с, движется в изогнутой трубе АВС, расположенной в вертикальной плоскости. На участке АВ на груз кроме силы тяжести P действует постоянная сила Q (Q=12Н). и сила сопротивления среды R, зависящая от скорости v груза, R=0.6·V2 (направлена против движения). В точке В груз, не меняя своей скорости, переходит на участок ВС трубы, где на него кроме силы тяжести действует переменная сила А, проекция которой на ось X: Fx =-5sin(2t). Считая груз материальной точкой и зная расстояние АВ=l=5м движения груза от точки А до точки В, найти закон движения груза на участке ВС, т.е. X=f(t), где X=ВD. Трением груза о трубу пренебречь. Вариант 44	Задача Д1 Груз D массой m, получив в точке А начальную скорость υ0, движется в изогнутой трубе ABC, расположенной в вертикальной плоскости; участки трубы или оба наклонные, или один горизонтальный, а другой наклонный (рис. Д1.0 – Д1.9, табл. Д1). На участке АВ, на груз кроме силы тяжести, действуют постоянная сила Q (ее направление показано на рисунках) и сила сопротивления среды R, зависящая от скорости v груза (направлена против движения); трением груза о трубу на участке АВ пренебречь. В точке В груз, не изменяя своей скорости, переходит на участок ВС трубы, где на него, кроме силы тяжести, действуют сила трения (коэффициент трения груза о трубу f = 0,2) и переменная сила F, проекция которой Fx на ось х задана в таблице. Считая груз материальной точкой и зная расстояние АВ = l или время t1 движения груза от точки А до точки В, найти закон движения груза на участке ВС, т. е. x = f(t), где x = BD Вариант 75
На тело 1 действует постоянная сила F. Определить ускорение этого тела в момент времени t, если относительно него под действием внутренних сил системы движется тело 2 согласно уравнению x=x(t). Тела движутся поступательно. Дано: m1=4кг, m2=1кг, t=0.5c, F=10H, x=sin(π*t).	Шкив 2 радиуса R, вращаясь с угловым ускорением ɛ2, поднимает однородный цилиндр 1, масса которого m (рис.10). Определить модуль главного вектора внешних сил, действующих на цилиндр 1. Дано: R=0.2м, ɛ2=10c-2, m=50кг;
По борту стоящего свободно на воде катера массы m1 и длины S с носа на корму переходит человек массы m2. Пренебрегая сопротивлением воды, определить направление и величину перемещения катера L. Дано: S=5м, m1=600кг, m2=80кг.	Задача Д1 Автомобиль М массой m имея в точке А начальную скорость V0, движется по трассе АВС и мосту СД. Участки АВ и ВС наклонные. На участке АВ на автомобиль действует постоянная сила трения Fтр, а также постоянная сила F. В точках В и С автомобиль не изменяет величину своей скорости. Мост образует дугу окружности радиуса R. Максимальный прогиб моста h. Считая автомобиль материальной точкой, определить: 1. Скорости автомобиля в точках В,С трассы и точке К моста 2. Силу давления автомобиля на мост, когда он находится в точке К 3. Установить, находится или нет автомобиль в точке К в отрыве от моста. Вариант 44
Задание Д-3 Механическая система, изображенная на рис. Д-3, состоит из нескольких тел, соединенных нерастяжимыми и не провисающими нитями; при этом тела системы совершают либо поступательное движение (грузы), либо вращаются вокруг неподвижной горизонтальной оси (однородные диски либо соосные блоки, жестко насаженные на единую ось), либо совершают плоскопараллельное движение (однородные диски либо соосные блоки). При выполнении задания необходимо: 1. Составить математическую модель для определения движений всех тел механической системы, а так же реакций внешних и внутренних связей в виде замкнутой системы дифференциальных и алгебраических уравнений. 2. Для указанного преподавателем тела получить дифференциальное уравнение движения. 3. Для указанного преподавателем тела получить дифференциальное уравнение движения, используя теорему об изменении кинетической энергии. 4. Решить полученное в пунктах 2 и 3 дифференциальное уравнение при заданных начальных условиях. 5. Получить математическую модель для анализа условий равновесия рассматриваемой механической системы.	Задача Д12-75 (Рисунок Д12.7, номер условия 5, С.М. Тарг 1989 г.)
По горизонтальной платформе длины S и массы m1, находившейся в начальный момент времени в покое, двое рабочих перекатывают тяжелый груз из левого конца платформы в правый. В какую сторону и насколько переместится при этом платформа, если общая масса груза и рабочих равна m2. Силами сопротивления движению пренебречь. Дано: S=6м, m1=3500кг, m2=1500кг.	ЗАДАНИЕ Д2 Механическая система состоит из прямоугольной вертикальной плиты 1 массой m1 = 24 кг и груза D массой m2 = 8 кг; плита или движется вдоль горизонтальных направляющих, или вращается вокруг вертикальной оси z, лежащей в плоскости плиты. В момент времени t0 груз начианет двигаться под действием внутренних сил по имеющемуся на плите желобу; закон его движения s=AD=F(t) задан в таблице. Плита имеет в момент t0 = 0 скорость u0 = 0. Считая груз материальной точкой и пренебрегая всеми сопротивлениями, определить указанное в столбцах 4 и 9 таблицы. Вариант 34