Артикул: 1151322

Раздел:Технические дисциплины (96540 шт.) >
  Теоретическая механика (теормех, термех) (1936 шт.) >
  Динамика (366 шт.)

Название или условие:
Практическое задание 6
«Теорема об изменении кинетической энергии механической системы»
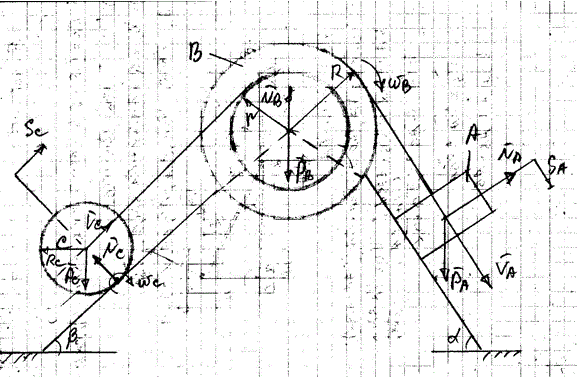
Механизм, состоящий из груза А, блока В (больший радиус – R, меньший – r, радиус инерции относительно центральной оси – i) и однородного круглого цилиндра С радиусом RC, установлен на призме, закрепленной на плоскости. Под действием сил тяжести из состояния покоя механизм пришел в движение. Качение цилиндра (блока) происходит без проскальзывания. Трения на неподвижной оси вращающегося блока (цилиндра) нет. Нити, соединяющие тела, параллельны плоскостям. Какую скорость развил груз А, переместившись на расстояние S_A?
Вариант 54 (Схема 22)
Дано: m_A=9кг, m_B=3кг, m_C=15кг, α=60°, β=45°, R_C=30см=0.3м, g≈9.8м/с², R=60см=0.6м, r=40см=0.4м, i=52см=0.52м, S_A=1м.
Определить: V_A-?

Описание:
Подробное решение в WORD

Изображение предварительного просмотра:

Процесс покупки очень прост и состоит всего из пары действий:
1. После нажатия кнопки «Купить» вы перейдете на сайт платежной системы, где можете выбрать наиболее удобный для вас способ оплаты (банковские карты, электронные деньги, с баланса мобильного телефона, через банкоматы, терминалы, в салонах сотовой связи и множество других способов)
2. После успешной оплаты нажмите ссылку «Вернуться в магазин» и вы снова окажетесь на странице описания задачи, где вместо зеленой кнопки «Купить» будет синяя кнопка «Скачать»
3. Если вы оплатили, но по каким-то причинам не смогли скачать заказ (например, случайно закрылось окно), то просто сообщите нам на почту или в чате артикул задачи, способ и время оплаты и мы отправим вам файл.
Условия доставки:
Получение файла осуществляется самостоятельно по ссылке, которая генерируется после оплаты. В случае технических сбоев или ошибок можно обратиться к администраторам в чате или на электронную почту и файл будет вам отправлен.
Условия отказа от заказа:
Отказаться возможно в случае несоответсвия полученного файла его описанию на странице заказа.
Возврат денежных средств осуществляется администраторами сайта по заявке в чате или на электронной почте в течении суток.

Похожие задания:

Найдите угловое ускорение тела (1)	Задача Д12-75 (Рисунок Д12.7, номер условия 5, С.М. Тарг 1989 г.)
Задача Д1 Груз D массой m, получив в точке А начальную скорость υ0, движется в изогнутой трубе ABC, расположенной в вертикальной плоскости; участки трубы или оба наклонные, или один горизонтальный, а другой наклонный (рис. Д1.0 – Д1.9, табл. Д1). На участке АВ, на груз кроме силы тяжести, действуют постоянная сила Q (ее направление показано на рисунках) и сила сопротивления среды R, зависящая от скорости v груза (направлена против движения); трением груза о трубу на участке АВ пренебречь. В точке В груз, не изменяя своей скорости, переходит на участок ВС трубы, где на него, кроме силы тяжести, действуют сила трения (коэффициент трения груза о трубу f = 0,2) и переменная сила F, проекция которой Fx на ось х задана в таблице. Считая груз материальной точкой и зная расстояние АВ = l или время t1 движения груза от точки А до точки В, найти закон движения груза на участке ВС, т. е. x = f(t), где x = BD Вариант 75	Задача Д2 4.2.1. Условия задачи. Механическая система (рис. 4.3) включает два ступенчатых шкива 1,2, обмотанных нитями, грузы 3, 4, 5, 6, прикрепленные к этим нитям, и невесомый блок, предназначенный для изменения направления нити. Система движется в вертикальной плоскости под действием сил тяжести грузов и пары сил с моментом М, приложенной к одному из шкивов. Радиусы внешних ступеней шкивов R1 и R2, веса шкивов Р1, Р2 и грузов Р3, Р4, Р5, Р6, а также величина момента М для конкретных вариантов задачи приведены в табл. Д2. Радиусы внутренних ступеней шкивов ri = 0,5Ri (i = 1,2), радиусы инерции шкивов относительно осей вращения ρi = 0,6Ri. Пренебрегая силами трения и считая нити нерастяжимыми, определить: - линейные ускорения грузов; - угловые ускорения шкивов; - силы натяжения нитей на участках между грузами и шкивами. Провести проверку и оценить погрешность решения с помощью уравнения движения шкива, к которому приложен момент М. Вариант 789
Найдите ускорение тела (1)	Задача Д1 Автомобиль М массой m имея в точке А начальную скорость V0, движется по трассе АВС и мосту СД. Участки АВ и ВС наклонные. На участке АВ на автомобиль действует постоянная сила трения Fтр, а также постоянная сила F. В точках В и С автомобиль не изменяет величину своей скорости. Мост образует дугу окружности радиуса R. Максимальный прогиб моста h. Считая автомобиль материальной точкой, определить: 1. Скорости автомобиля в точках В,С трассы и точке К моста 2. Силу давления автомобиля на мост, когда он находится в точке К 3. Установить, находится или нет автомобиль в точке К в отрыве от моста. Вариант 88
Задача 25 Груз массой m, двигаясь по наклонной плоскости, под действием силы F проходит путь S за время t. Считая движение груза равноускоренным с начальной скоростью V0 = 0 м/с, определить величину силы F, если коэффициент трения равен f.	Динамика точки. Вариант 8 На тело массой m, движущееся по горизонтальной гладкой поверхности вдоль оси x, действует сила, проекция которой равна Fx = −0,5x. В начальный момент x0 = 0, v0x = 10 м⁄с. Определить максимальное значение координаты x тела
Задача Д1 Автомобиль М массой m имея в точке А начальную скорость V0, движется по трассе АВС и мосту СД. Участки АВ и ВС наклонные. На участке АВ на автомобиль действует постоянная сила трения Fтр, а также постоянная сила F. В точках В и С автомобиль не изменяет величину своей скорости. Мост образует дугу окружности радиуса R. Максимальный прогиб моста h. Считая автомобиль материальной точкой, определить: 1. Скорости автомобиля в точках В,С трассы и точке К моста 2. Силу давления автомобиля на мост, когда он находится в точке К 3. Установить, находится или нет автомобиль в точке К в отрыве от моста. Вариант 33	Общие теоремы динамики материальной точки Шарик массы m движется из положения А внутри изогнутой трубки, расположенной в вертикальной плоскости. Шарик, пройдя путь 1, отделяется от пружины. В точке В шарик, не меняя значения своей скорости, переходит на участок ВС, где на него дополнительно действует переменная сила F, направление которой указано на рисунке. Пользуясь общими теоремами динамики точки, определить скорость шарика в положениях В и С. В задании приняты следующие обозначения: 1 - начальная скорость шарика, АВ - длина участка, 7 - время движения на участке ВС, f - коэффициент трения скольжения шарика по стенке трубки, с коэффициент жесткости пружины. Вариант 8