Артикул: 1034370
Раздел:Технические дисциплины (57837 шт.) >Теоретическая механика (теормех, термех) (1461 шт.) >
Динамика (237 шт.)
Название или условие:
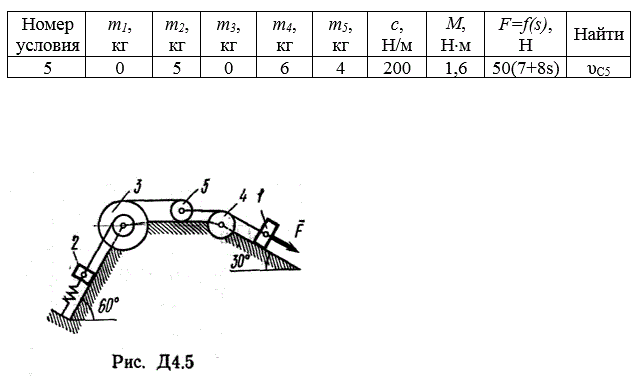
Механическая система состоит из грузов 1 и 2, ступенчатого шкива 3 с радиусами ступеней R3 = 0,3 м, r3 = 0,1 м и радиусом инерции относительно оси вращения ρ3 = 0,2м, блока 4 радиуса R4 = 0,2 м и катка (или подвижного блока) 5 (рис. Д4.0 – Д4.9, табл. Д4); тело 5 считать сплошным однородным цилиндром, а массу блока 4 – равномерно распределенной по ободу. Коэффициент трения грузов о плоскость f = 0,1. Тела системы соединены друг с другом нитями, перекинутыми через блоки и намотанными на шкив 3 (или на шкив и каток); участки нитей параллельны соответствующим плоскостям. К одному из тел прикреплена пружина с коэффициентом жесткости с.
Под действием силы F = f(s), зависящей от перемещения s точки ее приложения, система приходит в движение из состояния покоя; деформация пружины в момент начала движения равна нулю. При движении на шкив 3 действует постоянный момент М сил сопротивления (от трения в подшипниках).
Определить значение искомой величины в тот момент времени, когда перемещение s станет равным s1 = 0,2 м. Искомая величина указана в столбце «Найти» таблицы, где обозначено: υ1, υ2, υС5 – скорости грузов 1, 2 и центра масс тела 5 соответственно, ω3 и ω4 – угловые скорости тел 3 и 4.
Все катки, включая и катки, обмотанные нитями (как, например, каток 5 на рис. 1), катятся по плоскостям без скольжения.
На всех рисунках не изображать груз 2, если m2=0; остальные тела должны изображаться и тогда, когда их масса равна нулю.
Описание:
Указания. Задача Д4 – на применение теоремы об изменении кинетической энергии системы. При решении задачи учесть, что кинетическая энергия Т системы равна сумме кинетических энергий всех входящих в систему тел; эту энергию нужно выразить через ту скорость (линейную или угловую), которую в задаче надо определить. При вычислении Т для установления зависимости между скоростями точек тела, движущегося плоскопараллельно, или между его угловой скоростью и скоростью центра масс воспользоваться мгновенным центром скоростей (кинематика). При вычислении работы надо все перемещения выразить через заданное перемещение s1, учтя, что зависимость между перемещениями здесь будет такой же, как между соответствующими скоростями.
Подробное решение в WORD
Поисковые тэги: Задачник Тарга 1989г.
Изображение предварительного просмотра:
Процесс покупки очень прост и состоит всего из пары действий:
1. После нажатия кнопки «Купить» вы перейдете на сайт платежной системы, где можете выбрать наиболее удобный для вас способ оплаты (банковские карты, электронные деньги, с баланса мобильного телефона, через банкоматы, терминалы, в салонах сотовой связи и множество других способов)
2. После успешной оплаты нажмите ссылку «Вернуться в магазин» и вы снова окажетесь на странице описания задачи, где вместо зеленой кнопки «Купить» будет синяя кнопка «Скачать»
3. Если вы оплатили, но по каким-то причинам не смогли скачать заказ (например, случайно закрылось окно), то просто сообщите нам на почту или в чате артикул задачи, способ и время оплаты и мы отправим вам файл. Условия доставки: Получение файла осуществляется самостоятельно по ссылке, которая генерируется после оплаты. В случае технических сбоев или ошибок можно обратиться к администраторам в чате или на электронную почту и файл будет вам отправлен. Условия отказа от заказа: Отказаться возможно в случае несоответсвия полученного файла его описанию на странице заказа. Возврат денежных средств осуществляется администраторами сайта по заявке в чате или на электронной почте в течении суток.
