Артикул: 1168096
Раздел:Технические дисциплины (111593 шт.) >Теоретические основы электротехники (ТОЭ) (25399 шт.) >
Переходные процессы (3598 шт.) >
постоянный ток (2745 шт.) >
второго рода (1349 шт.)
Название или условие:
Лабораторная работа № 22
ИССЛЕДОВАНИЕ ПЕРЕХОДНЫХ ПРОЦЕССОВ В ЦЕПИ R, L, C
22.1. Цель работы.
1. Исследование влияния сопротивления резистора R на характер и продолжительность переходного процесса при включении цепи R, L, C к источнику постоянной ЭДС.
2. Исследование влияния сопротивления резистора R и начальной фазы α на характер, продолжительность и интенсивность переходного процесса при включении цепи R, L, C к источнику синусоидальной ЭДС e(t) = Em•sin(ω t + α).
Вариант 3
Описание:
22.2. Исходные данные
Заданы:
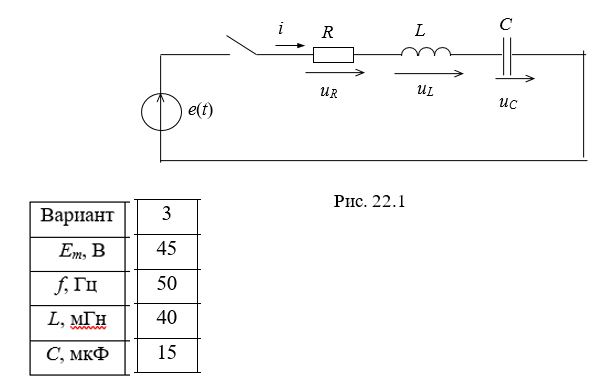
1. Эквивалентная схема исследуемой цепи, состоящая из источника ЭДС, резистора R, катушки индуктивности L и конденсатора C (рис. 22.1).
2. Параметры элементов схемы (табл. 22.1).
3. Рабочая схема исследуемой цепи и схема включения измерительных приборов (рис. 22.2).
22.4. Расчетная часть
1. Определить в общем виде функцию i(t) в переходном режиме при включении схемы с нулевыми начальными условиями к источнику постоянной ЭДС e(t) = Еm = const. Найти в общем виде выражение для корней характеристического уравнения. Определить значение критического сопротивления Rкр.
2. Для значения сопротивления резистора R = 2Rкр определить корни характеристического уравнения р1 и р2, расчетную продолжительность переходного процесса Тп. Результаты расчетов внести в табл. 22.2.
3. Для значения сопротивления резистора R = Rкр определить корни характеристического уравнения р1 = р2 = р, расчетную продолжительность переходного процесса Тп. Результаты расчетов внести в табл. 22.2.
4. Для значения сопротивления резистора R = 0,3 Rкр определить корни характеристического уравнения р1 и р2, расчетную продолжительность переходного процесса Тп, период собственных колебаний Т0. Результаты расчетов внести в табл. 22.2.
5. В выбранных масштабах mi и mt построить в одной системе координат семейство графических диаграмм исследуемой функции i(t) в переходном режиме для 3-х значений сопротивления резистора согласно п.п. 2, 3, 4. Построение диаграмм выполнить на ЭВМ.
6. Определить графически для каждого из 3-х значений сопротивления резистора согласно п.п. 2, 3, 4 расчетную продолжительность переходного процесса Тп, период собственных колебаний Т0. Результаты расчетов внести в
табл. 22.2.
7. Определить в общем виде функцию i(t) и в переходном режиме при включении схемы с нулевыми начальными условиями к источнику синусоидальной ЭДС e(t) = Em•sin(ωt +α).
8. Для значения сопротивления резистора R = 2 Rкр определить амплитуду установившейся составляющей тока Im и фазный угол φ на входе всей схемы. Результаты расчетов внести в табл. 22.3.
9. В выбранных масштабах mi и mt построить графическую диаграмму исследуемой функции i(t) в переходном режиме для значения начальной фазы источника α = φ согласно п.8. Построение диаграммы выполнить на ЭВМ. На диаграмме выделить установившуюся составляющую тока iу(t) =Im•sin(ω+0).
10. Для значения сопротивления резистора R = 0,3 Rкр определить амплитуду установившейся составляющей тока Im и фазный угол φ на входе всей схемы. Результаты расчетов внести в табл. 22.3.
11. В выбранных масштабах mi и mt построить графическую диаграмму исследуемой функции i(t) в переходном режиме для значения начальной фазы источника α = φ согласно п.8. Построение диаграммы выполнить на ЭВМ. На диаграмме выделить установившуюся составляющую тока iу(t) = Im•sin(ωt+0).
Подробное решение в WORD (12 страниц)+файл MathCad
Поисковые тэги: Классический метод
Изображение предварительного просмотра:
Процесс покупки очень прост и состоит всего из пары действий:
1. После нажатия кнопки «Купить» вы перейдете на сайт платежной системы, где можете выбрать наиболее удобный для вас способ оплаты (банковские карты, электронные деньги, с баланса мобильного телефона, через банкоматы, терминалы, в салонах сотовой связи и множество других способов)
2. После успешной оплаты нажмите ссылку «Вернуться в магазин» и вы снова окажетесь на странице описания задачи, где вместо зеленой кнопки «Купить» будет синяя кнопка «Скачать»
3. Если вы оплатили, но по каким-то причинам не смогли скачать заказ (например, случайно закрылось окно), то просто сообщите нам на почту или в чате артикул задачи, способ и время оплаты и мы отправим вам файл. Условия доставки: Получение файла осуществляется самостоятельно по ссылке, которая генерируется после оплаты. В случае технических сбоев или ошибок можно обратиться к администраторам в чате или на электронную почту и файл будет вам отправлен. Условия отказа от заказа: Отказаться возможно в случае несоответсвия полученного файла его описанию на странице заказа. Возврат денежных средств осуществляется администраторами сайта по заявке в чате или на электронной почте в течении суток.
