Артикул: 1167131

Раздел:Технические дисциплины (110628 шт.) >
  Сопротивление материалов (сопромат) (766 шт.) >
  Плоские балки (брусья) (341 шт.)

Название или условие:
Задача 5
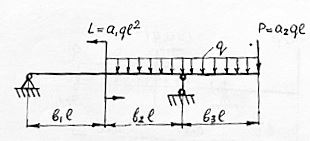
Построить эпюры поперечных сил и изгибающих моментов; установить опасное сечение, выполнить проектировочный расчет на прочность для трех типов сечений балки:
1) Определить необходимый диаметр сплошного круглого сечения;
2) Определить необходимые размеры прямоугольного сечения с соотношением сторон h = 2b;
3) Подобрать необходимый номер двутавра
4) Дать оценку экономичности сечений по весу погонного метра балки сделать вывод о рациональности сечений балки
5) Определить необходимые размеры сечения балки, если материал балки -чугун, для которого допускаемое напряжение при растяжении равно 30 МПа, на сжатии – 80 МПа. Построить эпюры нормальных и касательных напряжений для опасных сечений балки, определяя их максимальное значения.
Дано: q = 24 кН/м; l = 1,8 м; а1=3, а2=2; в1=0,5; в2=2; в3=1,5, сталь с допускаемым напряжением 160 МПа.

Описание:
Подробное решение в WORD

Изображение предварительного просмотра:

Процесс покупки очень прост и состоит всего из пары действий:
1. После нажатия кнопки «Купить» вы перейдете на сайт платежной системы, где можете выбрать наиболее удобный для вас способ оплаты (банковские карты, электронные деньги, с баланса мобильного телефона, через банкоматы, терминалы, в салонах сотовой связи и множество других способов)
2. После успешной оплаты нажмите ссылку «Вернуться в магазин» и вы снова окажетесь на странице описания задачи, где вместо зеленой кнопки «Купить» будет синяя кнопка «Скачать»
3. Если вы оплатили, но по каким-то причинам не смогли скачать заказ (например, случайно закрылось окно), то просто сообщите нам на почту или в чате артикул задачи, способ и время оплаты и мы отправим вам файл.
Условия доставки:
Получение файла осуществляется самостоятельно по ссылке, которая генерируется после оплаты. В случае технических сбоев или ошибок можно обратиться к администраторам в чате или на электронную почту и файл будет вам отправлен.
Условия отказа от заказа:
Отказаться возможно в случае несоответсвия полученного файла его описанию на странице заказа.
Возврат денежных средств осуществляется администраторами сайта по заявке в чате или на электронной почте в течении суток.

Похожие задания:

Необходимо: 1. Построить эпюры продольных сил и изгибающих моментов. 2. Найти [q] при b = 2 см, L = 110 см, σТ = 480 МПа, nT = 3. Результат представить в [Н/м] .	Задание 2 Требуется: а) подобрать размеры поперечного сечения балок. б) вычислить наибольшие нормальные и касательные напряжения при выбранных размерах поперечного сечения и сопоставить их с допускаемыми в) вычислить нормальные и касательные напряжения в заданной точке балки прямоугольного поперечного сечения. Вариант 3 Дано: М=24 кНм; а=2м; F=28 кН; q=10 кН/м
Необходимо: 1. Построить эпюры продольных сил и изгибающих моментов. 2. Найти [q] при b = 2 см, L = 100 см, σТ = 510 МПа, nT = 3. Результат представить в [Н/м] .	Необходимо: 1. Построить эпюры продольных сил и изгибающих моментов. 2. Найти [b] при q = 70000 Н/м, L = 120 см, σТ = 510 МПа, nT = 3. Результат представить в [м] .
Необходимо: 1. Построить эпюры продольных сил и изгибающих моментов. 2. Найти [q] при b = 4 см, L = 110 см, σТ = 400 МПа, nT = 2. Результат представить в [Н/м] .	Задача 34. Для стальной консольной балки с одним защемленным концом построить эпюры поперечных сил QY и изгибающих моментов МX. Подобрать сечение балки в двух вариантах: а) прокатный двутавр по ГОСТ 8240-72; б) прямоугольник с отношением сторон h/b=4/3. Определить отношение массы балки прямоугольного сечения к массе балки двутаврового сечения. Допускаемое нормальное напряжение при изгибе [σи]=160 МПа.
Задача 4 Абсолютно жесткий брус крепится к основанию при помощи шарнира и двух стальных стержней (σadmt=σadmc=160 МПа). Из условия прочности при осевом растяжении (сжатии) требуется: а) определить грузоподъемность заданной конструкции F; б) определить величины внутренних продольных сил и напряжений в стальных стержнях при нагружении конструкции силой F (вычисленной в п. “а”). Дано: a=0,9 м, b=1,1 м, c=0,8 м, d=0,8 м, e=2,8 м, A1=10см2, A2=12см2, схема 0.	Задачи на плоский поперечный изгиб балки Требуется построить эпюры поперечных сил и изгибающих моментов; подобрать указанные рядом с номером задачи сечения из условия прочности. В задаче IV в опасных сечениях построить эпюры нормальных и касательных напряжений. Общие исходные данные для всех задач на плоский поперечный изгиб: l = 6м, F = 48 кН, q = 12 кН/м, M = 18 кНм, σadm = 160 МПа.
Изгиб балок Задача 5 Условия задачи. Для заданных двух схем балок требуется: 1. Записать аналитические выражения (функции) для поперечных сил Q и изгибающих моментов М для каждого участка в общем виде, построить эпюры Q и M, найти максимальный по модулю изгибающий момент |M|max. 2. Подобрать для схемы «а» деревянную балку прямоугольного поперечного сечения с заданным отношением k высоты к ширине при допускаемом напряжении [σ] = 8 МПа, для схемы «б» – стальную балку двутаврового поперечного сечения при [σ] = 160 МПа. При подборе стальной балки допускается перегрузка, не превышающая 5%. Вариант 789 Дано: l1=0,8 м; l2=1,2 м; a=1,4 м M=14 кНм; P=8 кН; q=8 кН/м k=h/b=1,2	Необходимо: 1. Построить эпюры поперечных сил и изгибающих моментов. 2. Найти [b] при q = 3000 Н/м, L = 100 см, σТ = 360 МПа, nT = 2. Результат представить в [м] .