Артикул: 1167068

Раздел:Технические дисциплины (110565 шт.) >
  Теоретические основы электротехники (ТОЭ) (24657 шт.) >
  Переходные процессы (3487 шт.) >
  постоянный ток (2672 шт.) >
  второго рода (1311 шт.)

Название или условие:
Расчет переходных процессов в линейных цепях с сосредоточенными параметрами
Для вариантов схем, имеющих параметры, указанные в таблице, выполнить следующие расчеты:
1. Определить в переходном режиме при включении рубильника 2, операторным методом токи i1(t), i2(t), i3 (t) и напряжение на конденсаторе uC(t) учитывая, что рубильник 2 включается после рубильника 1, спустя время τ;
Вариант 497
Дано: Вычисляемая функция – huС(t)
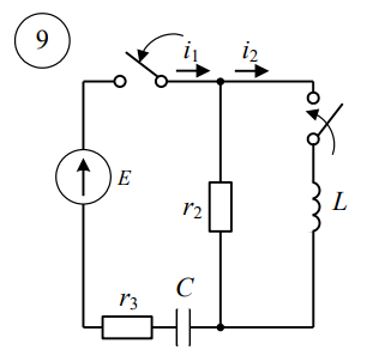
Схема 9
R1 = 0; R2 = 50 Ом; R = 50 Ом.
C = 180 мкФ.

Описание:
Указания
1. Для определения начальных условий необходимо провести предварительный расчёт схемы классическим методом в переходном режиме при разомкнутом рубильнике 2 и замкнутом рубильнике 1;
2. Величину времени τ рассчитать, используя корни характеристического уравнения, составленного при расчёте схемы классическим методом.
В случае колебательного процесса τ=T0/8, где Т0 – период собственных колебаний: T0=1/f0 , f0=1/(2π√LC),т.е.τ1=(2π√LC)/8;
В случае апериодического процесса с двумя корнями τi=1/|p1| , где p1 – меньший по модулю корень характеристического уравнения.
В случае апериодического процесса с одним корнем τi=1/|p| .
2. Используя формулу включения, определить переходную характеристику, указанную в таблице, при условии, что рубильник 2 замкнут, а рубильник 1 работает на замыкание (схема с нулевыми начальными условиями).
Е=100 [В], L=125 [мГн].


Поисковые тэги: Операторный метод, Классический метод

Изображение предварительного просмотра:

Процесс покупки очень прост и состоит всего из пары действий:
1. После нажатия кнопки «Купить» вы перейдете на сайт платежной системы, где можете выбрать наиболее удобный для вас способ оплаты (банковские карты, электронные деньги, с баланса мобильного телефона, через банкоматы, терминалы, в салонах сотовой связи и множество других способов)
2. После успешной оплаты нажмите ссылку «Вернуться в магазин» и вы снова окажетесь на странице описания задачи, где вместо зеленой кнопки «Купить» будет синяя кнопка «Скачать»
3. Если вы оплатили, но по каким-то причинам не смогли скачать заказ (например, случайно закрылось окно), то просто сообщите нам на почту или в чате артикул задачи, способ и время оплаты и мы отправим вам файл.
Условия доставки:
Получение файла осуществляется самостоятельно по ссылке, которая генерируется после оплаты. В случае технических сбоев или ошибок можно обратиться к администраторам в чате или на электронную почту и файл будет вам отправлен.
Условия отказа от заказа:
Отказаться возможно в случае несоответсвия полученного файла его описанию на странице заказа.
Возврат денежных средств осуществляется администраторами сайта по заявке в чате или на электронной почте в течении суток.

Похожие задания:

Задача № 1.2.3 из сборника Бычкова При t=0 в цепи замыкается ключ K. Найти независимые начальные условия, составить уравнения состояния. Для t>0 найти uc и iL, использовав аналитическое решение уравнений состояния, а также численное - по методу Эйлера. Затем найти uL и ic, использовав уравнения связи, и провести проверку полученных результатов (по ВАХ накопителей). Вариант 2 Цепь: 116-ИН U1=1; 212-R2=1; 323-С=0.5; 435 - K, размыкается; 556 - R5=1, замыкается; 634-L=1; 746 - R7=1; 846 -ИТ i8=4;	Для электрической цепи, питающейся от источника постоянной ЭДС Е, в которой происходит коммутация, выполнить следующее: 1. Определить закон изменения электрической величины (в соответствии с заданием) во времени после коммутации; 2. Построить график изменения искомой величины в функции времени. Вариант 21 Дано: Рисунок 5 E = 100 В; L = 1 мГн; C = 10 мкФ; R1 = 20 Ом; R2 = 20 Ом; R3 = 0; R4 = 2 Ом. Определить UL.
Вариант 1 Дано: R1 = 1 Ом; R2 = 1 Ом; R3 = 1 Ом; L = 1 Гн; C = 1 Ф; U0 = 3 В. Определить: uC; iL; i.	Найти минимальное значение емкости С2, при котором переходный процесс будет апериодическим для следующей схемы с параметрами U=1 В, R1=100 Ом; R2=10 Ом; L2=2 мГн. Ответ записать в мкФ, округлить до целых.
Рассчитать переходный процесс (для случая колебательного процесса) и изобразить операторную схему замещения.	Дана электрическая цепь, в которой происходит коммутация. В цепи действует постоянная ЭДС Е. Требуется определить закон изменения во времени тока после коммутации в одной из ветвей схемы или напряжения на каком-либо элементе или между заданными точками схемы. Задачу следует решать двумя методами: классическим и операторным. На основании полученного аналитического выражения требуется построить график изменения искомой величины в функции времени в интервале от t = 0 до t = 3/|p|min , где |p|min – меньший по модулю корень характеристического уравнения. Вариант 8
Определить начальные условия Установившийся режим. Характеристическое уравнение.	• Составить систему для поиска A1 и A2 • И характеристическое уравнение
ЗАДАЧА 5.1 Классический метод анализа переходных процессов В цепи (рис. 5.1) с параметрами (табл. 5.1) и источником постоянной ЭДС E=U требуется: 1. Для аналитического расчета переходного процесса 1.1. Составить систему дифференциальных уравнений (СЛДУ) в нормальной форме Коши, описывающих процессы в послекоммутационной схеме, относительно переменных состояния цепи. 1.2. Рассчитать переменные состояния, т.е. решить аналитически полученную систему уравнений динамики цепи. 1.3. Найти мгновенные значения остальных переменных цепи (токи и напряжения элементов, потокосцепления катушек, заряды конденсаторов), выразив их через переменные состояния (без производных и интегралов). 2. Записать СЛДУ цепи для численного интегрирование методом Эйлера. Выполнить процедуру на протяжении 10 – 15 шагов и полученные значения величин записать в соответствующую таблицу. Рекомендуется использовать ПК. 3. Построить графики переменных состояния цепи и всех токов цепи, приведя таблицу расчетных точек этих величин. На графики переменных состояния нанести кривые, подученные в результате численного интегрирования уравнений цепи. Оценить точность численного метода, указать характер, время переходного процесса, экстремальные значения функций, а в случае колебательного характера процесса – период и декремент колебаний. Вариант 10 Схема 10 Дано: E=U=60 В; L1=0,2 Гн; L2=0,1 Гн; R1=80 Ом; R2=70 Ом; M=0.1 Гн	ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ Для заданной электрической цепи (рис.4-1…4-14) и данным таблицы 1, согласно варианта, определить закон изменения во времени величины указанной в таблице. Задачу следует решать двумя методами: классическим и операторным. На основании полученного аналитического выражения требуется построить график изменения искомой величины в функции времени в интервале от t = 0 до t = 3/|p|min. Здесь |p|min – меньший по модулю корень характеристического уравнения. Вариант 32