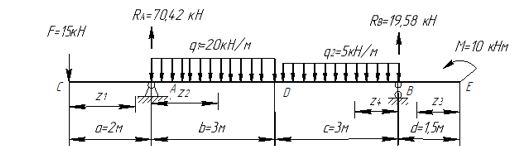
РГР5 задача на изгиб
Условие: Для загруженной стальной балки:
а) построить эпюры поперечных сил и изгибающих моментов;
б) подобрать размеры балки указанного профиля из условия прочности по нормальным напряжениям;
в) проверить выбранное сечение по касательным напряжениям;
г) построить эпюры нормальных и касательных напряжений для указанного сечения;
д) вычислить прогиб и угол поворота для указанных сечений.
Расчетную схему формировать на основании рисунка, изображенного ниже, и «дано»
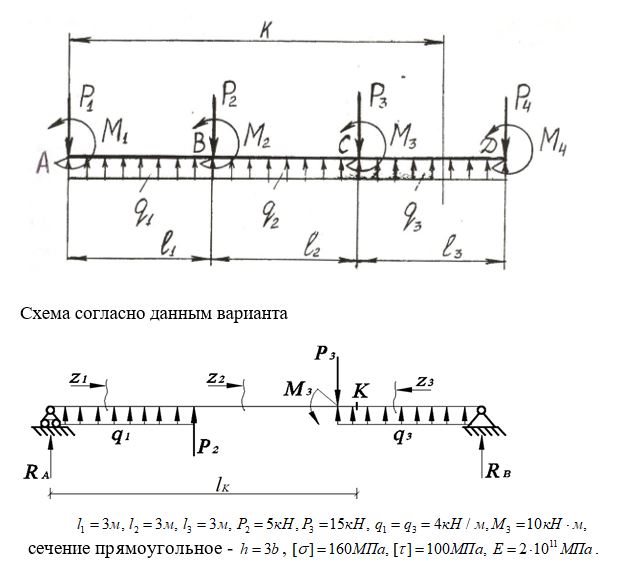 | Задача №9 Косой изгиб
Схема 9/ Строка 9
Для заданной балки требуется:
1) определить положение нейтральной линии и построить эпюру результирующих нормальных напряжений σ в опасном сечении балки;
2) проверить прочность по нормальным напряжениям, если [σ]=160 МПа;
У3) определить величину и направление полного прогиба в сечении под силой Р.
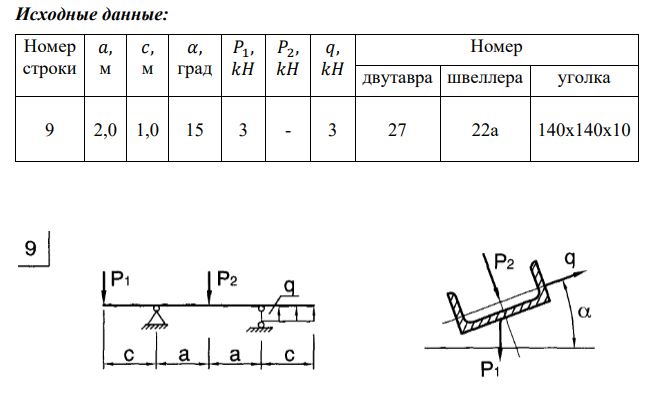 |
Контрольная работа №1
«Расчет на прочность статически определимой балки»
Статически определимая балка в конструкциях подвергается деформации плоского поперечного изгиба под действием внешних нагрузок: сосредоточенной силы F, равномерно распределенной по длине балки нагрузки интенсивностью q, сосредоточенного изгибающего момента m0. Приложение нагрузок по длине балки характеризуется линейными величинами l1, l2, l3 (рис. 1.1).
Необходимо подобрать стальную балку стандартного двутаврового сечения, удовлетворяющую требованиям работоспособности по критерию прочности в заданных условиях эксплуатации, а также построить эпюры нормальных и касательных напряжений по высоте опасных сечений.
Допускаемые касательные напряжения для сталей [τ] = 100 МПа.
Вариант 08
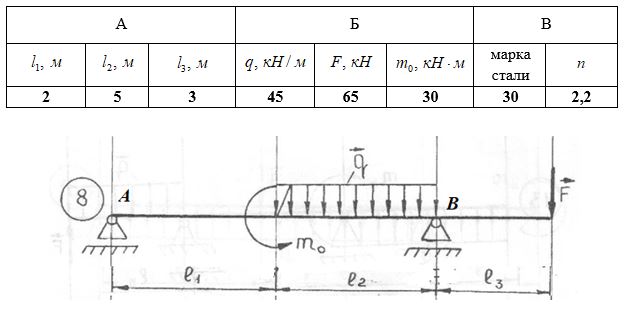 | Задача №2
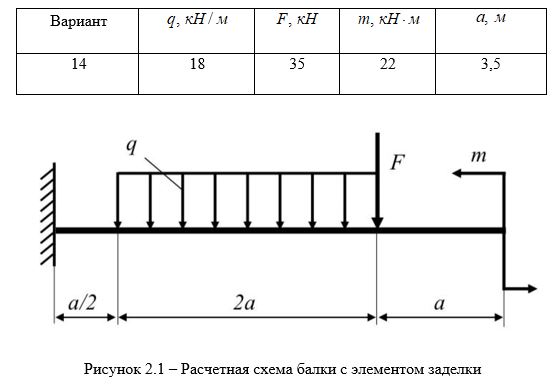
Для заданной балки построить эпюры поперечных сил и изгибающих моментов, подобрать из расчета на прочность номер двутавра, а также найти угол поворота на конце консоли. Принять допускаемое напряжение на изгиб [σ]=160 МПа, модуль упругости первого рода У = 2·105 МПа .
Вариант 14
 |
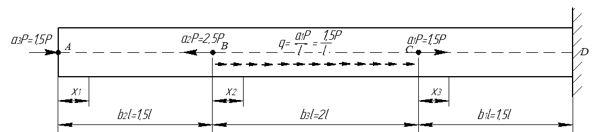
Задача 1. Для прямолинейного стержня, испытывающего растяжение-сжатие, построить эпюру продольной силы.
Исходные данные: а1 = 1,5; а2 =2,5; а3 = 1,5; в1 = 1,5; в2 = 1,5; в3 = 2
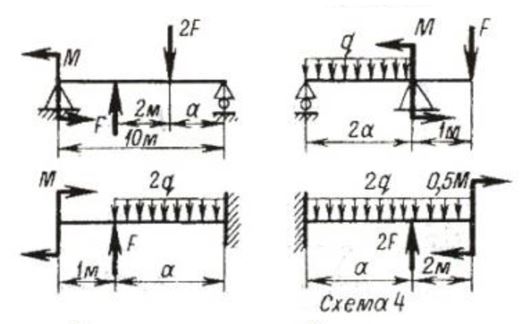
 | Требуется:
а) подобрать размеры поперечного сечения балок.
б) вычислить наибольшие нормальные и касательные напряжения при выбранных размерах поперечного сечения и сопоставить их с допускаемыми
в) вычислить нормальные и касательные напряжения в заданной точке балки прямоугольного поперечного сечения.
Вариант 4
Дано: М=24 кНм; а=2м; F=22 кН; q=6 кН/м
 |
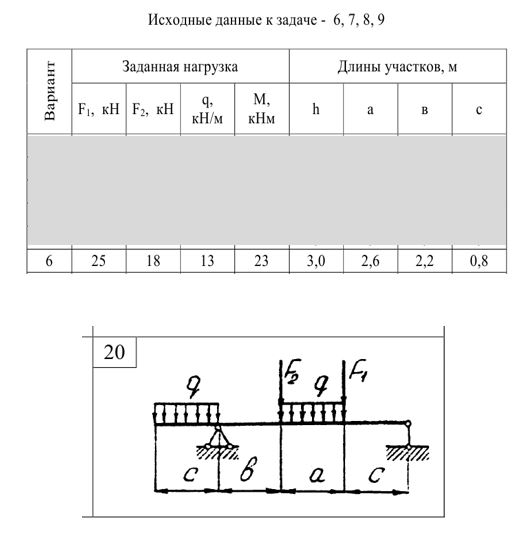
1. Для заданных схем статически определимых балок определить:
• опорные реакции и построить эпюры поперечных сил и изгибающих моментов;
2. В задаче 6 дополнительно:
• из условия прочности подобрать стальную балку двутаврового сечения;
• вычислить для нее максимальные значения нормального и касательного напряжений;
• в опасных сечениях построить эпюры изменения нормальных и касательных напряжений по высоте двутавровой балки;
• определить прогибы в характерных точках балки (середина пролета, точки приложения сил, крайние точки на консолях);
• по найденным точкам построить изогнутую ось балки. Вычислить так- же угол поворота сечения на правой опоре.
Вариант 6
 | Вариант 1.
Данные для задания:
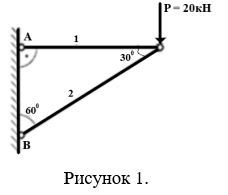
К кронштейну, состоящему из стальных стержней, в узле приложена сила Р = 20 кН. (Рис. 1). Определить усилие в стержнях – 1 и 2, и подобрать необходимые размеры сечения стержней из швеллера (прокатный профиль).
Размеры сечений первого и второго стержня принять одинаковыми.
Материал стержней – сталь, допустимое напряжение при растяжении и сжатии: [σ] = 160 МПа = 16 кН/см2 . Угол между стержнями α = 30°.
 |
Вариант 9
Задача 4.
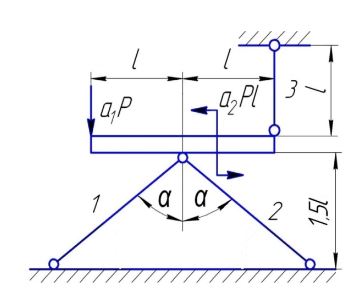
Исходя из условия прочности, определить допускаемую нагрузку [P], если площадь поперечного сечения первого стержня F1 = 10 см2, предел текучести материала стержней σт= 300 МПа, нормативный коэффициент запаса прочности по отношению к пределу текучести nт=2 Исходные данные: а1 = 1; а2 =1,5;α=60º F2=0,5 F1, F3 =0,75 F1, F4 =2,2 F1, F5 =2,5 F1,
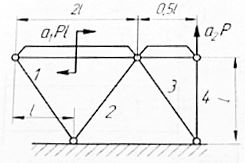
 | Задача 4. Исходя из условия прочности, определить допускаемую нагрузку [P], если площадь поперечного сечения первого стержня F1 = 10 см2, предел текучести материала стержней σт= 300 МПа, нормативный коэффициент запаса прочности по отношению к пределу текучести nт=2 Исходные данные: а1 = 1,5; а2 =2,5; F2=0,75 F1, F3 =F1, F4 =0,5 F1
 |