Артикул: 1107232

Раздел:Технические дисциплины (69660 шт.) >
  Теоретическая механика (теормех, термех) (1787 шт.) >
  Динамика (330 шт.)

Название или условие:
Задание 9. Принцип Даламбера
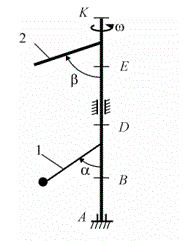
Вертикальный вал, вращающийся с постоянной угловой скоростью ω=10 (1/с), закреплен подпятником в точке А и цилиндрическим подшипником в точке B.
AB=BD=DE=EK=b=0,4 м
К валу жестко прикреплены невесомый стержень 1 длиной l1=0,4 м с точечной массой m1=6 кг на конце и однородный стержень 2 длиной l2=0,6 м, имеющий массу m2=4 кг. Вал и оба стержня лежат в одной плоскости.
Точки крепления стержней к валу: В для стержня 1, Е для стержня 2.
α=75° β=120°
Пренебрегая весом вала, определить реакции связей.
Вариант АБВ = 342

Описание:
1.Выбор исходных данных. Нанесение внешних сил на схему.
2. Принцип Даламбера. Нанесение на схему сил инерции. Нанесение на схему реакций опор.
3. Составление уравнений равновесия. Нахождение реакций опор.
4.Выводы.

Подробное решение в WORD - 3 страницы

Изображение предварительного просмотра:

Процесс покупки очень прост и состоит всего из пары действий:
1. После нажатия кнопки «Купить» вы перейдете на сайт платежной системы, где можете выбрать наиболее удобный для вас способ оплаты (банковские карты, электронные деньги, с баланса мобильного телефона, через банкоматы, терминалы, в салонах сотовой связи и множество других способов)
2. После успешной оплаты нажмите ссылку «Вернуться в магазин» и вы снова окажетесь на странице описания задачи, где вместо зеленой кнопки «Купить» будет синяя кнопка «Скачать»
3. Если вы оплатили, но по каким-то причинам не смогли скачать заказ (например, случайно закрылось окно), то просто сообщите нам на почту или в чате артикул задачи, способ и время оплаты и мы отправим вам файл.
Условия доставки:
Получение файла осуществляется самостоятельно по ссылке, которая генерируется после оплаты. В случае технических сбоев или ошибок мозно обратиться к администраторам в чате или на электронную почту и файл будет вам отправлен.
Условия отказа от заказа:
Отказаться возможно в случае несоответсвия поулченного файла его описанию на странице заказа.
Возврат денежных средств осуществляется администраторами сайта по заявке в чате или на электронной почте в течении суток.

Похожие задания:

Определить скорость V3	Задача Д1. Интегрирование ДУ движения материальной точки, находящейся под действием постоянных сил. Варианты 6-0 (рис.20 приложения, схема 2 и данные в таблице 32). Лыжник подходит к точке A участка трамплина AB, наклонённого под углом α к горизонту и имеющего длину l, со скоростью vA. Коэффициент трения скольжения лыж на участке AB равен f. Лыжник от A до B движется τ с; в точке B он покидает трамплин со скоростью vB. Через T с лыжник приземляется со скоростью vC в точке C горы, составляющей угол β с горизонтом. При решении задачи принять лыжника за материальную точку и не учитывать сопротивление воздуха Вариант 0
Лыжник массой m = 70 кг опускается без начальной скорости по склону, составляющему угол α = 30° с горизонтом, не отталкиваясь палками. Длина спуска l = 100 м, коэффициент трения скольжения лыж о снег f = 0.1. Сила сопротивления воздуха пропорциональна квадрату скорости R = 0.4v2. Определить скорость лыжника в конце спуска.	Практическое задание 7 «Общее уравнение динамики» Номер варианта задается преподавателем и соответствует номеру на рисунке. Для заданной механической системы определить ускорение груза. Массами нитей пренебречь. Трение качения и силы сопротивления в подшипниках не учитывать. Система движется из состояния покоя. Варианты механических систем показаны на рисунке, необходимые для решения данные приведены в таблице. Блоки и катки, для которых радиусы инерции в таблице указаны, считать сплошными однородными цилиндрами. Вариант 54 (Схема 24) Дано: G1=2*G, G2=G, G3=G, G4=8*G, R2=R3=r, g≈9.81м/с2. Найти: a1, T-?
Задание Д4. Исследование относительного движения материальной точки Шарик М, рассматриваемый как материальная точка, перемещается по цилиндрическому каналу движущегося тела А (рис. 11). Найти уравнение относительного движения этого шарика х = f(t), приняв за начало отсчета точку О. Тело А равномерно вращается вокруг неподвижной оси (ось вращения z1 вертикальна). Найти также координату х и давление шарика на стенку канала при заданном значении t = t1. Вариант 7 Дано: m = 0,03 кг; ω = 2π рад/с; х0 = 0,3 м; ; t1 = 0,2 с; h = 0,2 м; f = 0.	Задача 3.2 Вертикальный вал АВ (рис.1.2), вращающийся с постоянной угловой скоростью ω, закреплен подпятником в точке А и цилиндрическим подшипником в точке В К валу жестко прикреплен невесомый стержень длиной l с точечной массой m на конце. Пренебрегая весом вала, определить реакции подпятника А и подшипника В. Вариант 5 Дано: ω=10c-1-const, l=0.4м, a=b=0.6м, m=2кг, α=60°, g≈10м/c2. Определить: YA, ZA, RB-?
Найти: V3 с помощью общего уравнения динамики	Задача Д1 Динамика материальной точки Груз D массой m, получив в точке А начальную скорость, движется в изогнутой трубе АВС, расположенной в вертикальной плоскости. На участке АВ на груз кроме силы тяжести действует постоянная сила Q=10Н, направленная от точки А к точке В, и сила сопротивления среды R , зависящая от скорости V груза D: R=μVn. В точке В груз, изменив направление приобретенной скорости, но, сохранив при этом ее величину, переходит на участок ВС трубы, где на него, помимо силы тяжести действует сила трения (коэффициент трения груза о трубу f=0,2) и переменная по величине сила F=F(t), направленная вдоль участка ВС. Проекция Fx последней на ось Вх задается. Считая груз D материальной точкой, и зная расстояние АВ или время t движения груза от точки А до точки В, найти уравнение х=х(t) движения груза на участке ВС. Вариант 11-5
Для заданной механической системы требуется определить кинематическую величину (угловую скорость заданного тела или линейную скорость). ○Дано: F, Mc, m1, m2, m3, R2, R3, α. Звенья 2 и 3 – сплошные однородные цилиндры. Найти: скорость тела 1 - v1, в зависимости от пройденного пути с помощью теоремы об изменении кинетической энергии.	Задача 3.1 Груз массой m, получив в точке А начальную скорость V0, движется по гладкой горизонтальной поверхности под действием постоянной силы Q. На груз действует сила сопротивления R, зависящая от скорости груза. Определить скорость груза в момент времени t1. Вариант 5 Дано: R=µ*V=0.4*V(H), m=4кг, V0=20м/с, µ=0.4H*c/м, t1=5c, g≈9.81м/c2, Q=4H. Определить: V1-?