Артикул: 1054767
Раздел:Технические дисциплины (57837 шт.) >Теоретическая механика (теормех, термех) (1461 шт.) >
Динамика (237 шт.)
Название или условие:
Курсовая работа по Динамике
Вариант 10
Описание:
Методика выполнения курсовой работы
1. Определить направление движения системы тел 1 и 2 относительно призмы 3. для этого составить уравнения равновесия тел 1, 2, блока А и В. Из этих уравнений определить силы натяжения нитей и по сумме моментов этих сил относительно оси вращения одного из блоков А или В определить вращение этого блока. Для катящегося без скольжения катка уравнение условного равновесия составлять в виде суммы моментов относительно точки его соприкосновения с поверхностью призмы 3.
2. Определив, в каком направлении будут перемещаться тела 1 и 2, составить уравнения кинематических связей, то есть уравнения, связывающие между собой относительные линейны скорости и центров масса тел 1 и 2 системы угловые скорости блоков А и В, а также катка 1 или 2, совершающего плоскопараллельное движение. Обозначить относительное перемещение тела 1 как , найти через него, используя уравнения кинематических связей.
3. Расположив на горизонтальной поверхности упор, ограничивающий перемещение тела 3, написать теорему о движения центра масс системы в проекция на ось Ох. Далее определить горизонтальную реакцию этого упора, выразив ее как функцию ускорения тела 1.
4. В данном пункте и во всех последующих считать призму 3 относительно неподвижным основанием. Движение всех остальных тел по призме рассматривать происходящим при действии их сил тяжестей, а также силы F и момента М. Выполнить предварительный условно статический расчет по аналогии с п.1.
5. Составить дифференциальные уравнения движения каждого из тел системы. Все угловые и линейные ускорения в дифференциальных уравнениях выразить через ускорение центра масс тела 1. Из совместного решения дифференциальных уравнений найти ускорение , силы натяжения каждого из участков нити, силу трения сцепления катка 1( или 2), а по ней коэффициент трения.
6. Найти скорость как функцию перемещения и ускорение центра масс тела 1 с помощью теоремы об изменении кинетической энергии механической системы.
7. Найти ускорение центра масс тела с помощью общего уравнения динамики.
8. Найти ускорение центра масс тела 1 с помощью уравнения Лагранжа 2-ого рода.
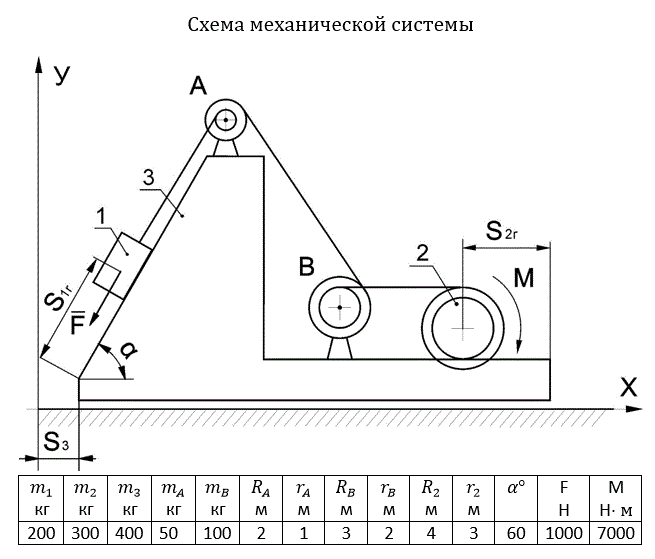
Схема механической системы 2
Методика выполнения курсовой работы 2
1 Предварительный расчет I 5
2 Теорема о движении центра масс 8
3 Теорема о движении центра масс 12
4 Предварительный расчет II 14
5 Дифференциальные уравнения движения 16
6 Теорема об изменении кинетической энергии механической системы 20
7 Общее уравнение динамики 22
8 Уравнение Лагранжа 2-го рода 24
Список литературы 27
Всего 28 страниц
Изображение предварительного просмотра:
Процесс покупки очень прост и состоит всего из пары действий:
1. После нажатия кнопки «Купить» вы перейдете на сайт платежной системы, где можете выбрать наиболее удобный для вас способ оплаты (банковские карты, электронные деньги, с баланса мобильного телефона, через банкоматы, терминалы, в салонах сотовой связи и множество других способов)
2. После успешной оплаты нажмите ссылку «Вернуться в магазин» и вы снова окажетесь на странице описания задачи, где вместо зеленой кнопки «Купить» будет синяя кнопка «Скачать»
3. Если вы оплатили, но по каким-то причинам не смогли скачать заказ (например, случайно закрылось окно), то просто сообщите нам на почту или в чате артикул задачи, способ и время оплаты и мы отправим вам файл. Условия доставки: Получение файла осуществляется самостоятельно по ссылке, которая генерируется после оплаты. В случае технических сбоев или ошибок можно обратиться к администраторам в чате или на электронную почту и файл будет вам отправлен. Условия отказа от заказа: Отказаться возможно в случае несоответсвия полученного файла его описанию на странице заказа. Возврат денежных средств осуществляется администраторами сайта по заявке в чате или на электронной почте в течении суток.
