Артикул: 1168525
Раздел:Технические дисциплины (112022 шт.) >Теоретические основы электротехники (ТОЭ) (25817 шт.) >
Цепи переменного синусоидального тока (6913 шт.)
Название или условие:
Лабораторная работа № 2
КОМПЬЮТЕРНЫЙ АНАЛИЗ ЧАСТОТНЫХ ХАРАКТЕРИСТИК ПОСЛЕДОВАТЕЛЬНОГО КОЛЕБАТЕЛЬНОГО КОНТУРА С ИСПОЛЬЗОВАНИЕМ ПРОГРАММЫ FASTMEAN
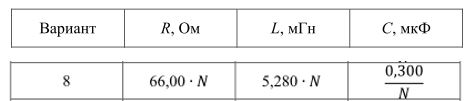
Вариант 8 N = 7
Описание:
1. Задание на самостоятельную подготовку
1.1. Изучите теоретические вопросы, связанные с явлением резонанса
в последовательном колебательном контуре.
1.2. Рассчитайте резонансную частоту f 0, добротность Q и ширину полосы пропускания 2Δf^* последовательного колебательного контура, схема которого приведена на рис. 2.1, по формулам
1.3. Рассчитайте частоты fmaxL и fmaxC, при которых напряжения индуктивности UL и емкости UC максимальны:
1.4. Рассчитайте на резонансной частоте значения амплитудно-частотных характеристик, соответствующих передаточным функциям:
Результаты расчетов занесите в графу «Предварительный расчет» табл. 2.2.
2. Задание для моделирования на компьютере
2.1. Загрузите программу FASTMEAN, предварительно изучив описание работы с программой.
2.2. Постройте на экране дисплея схему последовательного колебательного контура, приведенную на рис. 2.1, задайте значения параметров элементов, пронумеруйте узлы.
2.3. Рассчитайте и исследуйте влияние величины сопротивления R на частотные характеристики цепи, рассматривая в качестве выходной величины напряжение на резистивном сопротивлении R:
в диапазоне частот 1 Гц < f < 10 кГц. Для этого выберете в меню «Анализ» строку «Частотные характеристики» (рис. 2.2). Далее заполните таблицу анализа, как это показано на рис. 2.3.
Выберите начальную частоту 1 Гц, конечную частоту 10 кГц, число расчетных точек равным 1000, масштаб «линейный». Для изменения параметра R используйте опцию «параметр» в таблице «Частотные характеристики». В качестве начального значения R введите уменьшенное в 10 раз – 0,1R, а в качестве конечного – заданное значение R (рис. 2.4). Установите число графиков равное трем. Вы получите семейство резонансных кривых (рис. 2.5). Сохраните получившиеся графики.
2.4. Проведите детальный анализ частотных характеристик |HR(jω)| в узком диапазоне частот, включающем полосу пропускания, выделив часть графиков вблизи резонансной частоты (рис. 2.5). По полученным графикам, поочередно для каждого значения R (на рис. 2.6 показано, как изменить значение R), с помощью электронной линейки определите максимальное значение амплитудно-частотной характеристики |HR (jω)|max=|HR (jω0 )|, резонансную частоту f0, при которой |HR (jω)|, максимально, и граничные частоты f–1 и f 1 полосы пропускания.
Рассчитайте ширину полосы пропускания контура 2Δf*=f1-f(-1).
Полученные значения HR (jω0 ), f0 и 2Δf* занесите в графу «Результаты расчета на ПК» табл. 2.2. Обратите внимание, что максимальное значения АЧХ на резонансной частоте |HR(jω0)| не изменяется при различных значениях резистивного сопротивления R.
2.5. Рассчитайте одновременно амплитудно-частотные характеристики цепи, используя в качестве выходных величин напряжения на индуктивности и на емкости:
в диапазоне частот 1 Гц < f < 10 кГц, выбрав число расчетных точек равным 1000. Сохраните полученные резонансные кривые. На рис. 2.7 показаны настройки для получения |HL (jω)|, а на рис. 2.8 – для получения |HC (jω)|. Настройки «параметр» не изменяются и остаются такими же (см. рис. 2.4).
2.6. Проведите детальный анализ частотных характеристик, выделив часть графиков вблизи резонансной частоты, и найдите по ним с помощью линейки частоты fmaxL и fmaxC, при которых |HL (jω)| и |HC (jω)| принимают максимальные значения. Анализ проведите для трех значений R. Занесите значения fmaxL и f maxC в графу «Результаты расчета на ПК» табл. 2.2.
2.7. Найдите резонансную частоту f0. С помощью линейки определите значения амплитудно-частотных характеристик |HL (jω0)| и |HC (jω0 )| на резонансной частоте. Анализ проведите для трех значений R. Занесите значения |HL (jω0 )| и |HC (jω0 )| в табл. 2.2.
Подробное решение в WORD+файл MathCad+файл .scm
Поисковые тэги: Резонанс в контурах
Изображение предварительного просмотра:
Процесс покупки очень прост и состоит всего из пары действий:
1. После нажатия кнопки «Купить» вы перейдете на сайт платежной системы, где можете выбрать наиболее удобный для вас способ оплаты (банковские карты, электронные деньги, с баланса мобильного телефона, через банкоматы, терминалы, в салонах сотовой связи и множество других способов)
2. После успешной оплаты нажмите ссылку «Вернуться в магазин» и вы снова окажетесь на странице описания задачи, где вместо зеленой кнопки «Купить» будет синяя кнопка «Скачать»
3. Если вы оплатили, но по каким-то причинам не смогли скачать заказ (например, случайно закрылось окно), то просто сообщите нам на почту или в чате артикул задачи, способ и время оплаты и мы отправим вам файл. Условия доставки: Получение файла осуществляется самостоятельно по ссылке, которая генерируется после оплаты. В случае технических сбоев или ошибок можно обратиться к администраторам в чате или на электронную почту и файл будет вам отправлен. Условия отказа от заказа: Отказаться возможно в случае несоответсвия полученного файла его описанию на странице заказа. Возврат денежных средств осуществляется администраторами сайта по заявке в чате или на электронной почте в течении суток.
