Артикул: 1166863
Раздел:Технические дисциплины (110363 шт.) >Теоретические основы электротехники (ТОЭ) (24495 шт.) >
Цепи постоянного тока (4843 шт.)
Название или условие:
Задание № 1
ЛИНЕЙНЫЕ ЦЕПИ ПОСТОЯННОГО ТОКА
Для электрической схемы, соответствующей номеру варианта, выполнить следующее:
1. Составить на основании законов Кирхгофа систему уравнений для расчёта токов во всех ветвях схемы.
2. Определить токи во всех ветвях схемы методом контурных токов.
3. Определить токи во всех ветвях схемы методом узловых потенциалов.
4. Результаты расчета токов, проведенного двумя методами, свести в таблицу и сравнить их между собой.
5. Составить баланс мощностей в исходной схеме, вычислив суммарную мощность источников и суммарную мощность нагрузок (сопротивлений).
6. Определить ток I1 в заданной по условию схеме, используя теорему об активном двухполюснике и эквивалентном генераторе.
7. Начертить потенциальную диаграмму для любого замкнутого контура, включающего обе ЭДС.
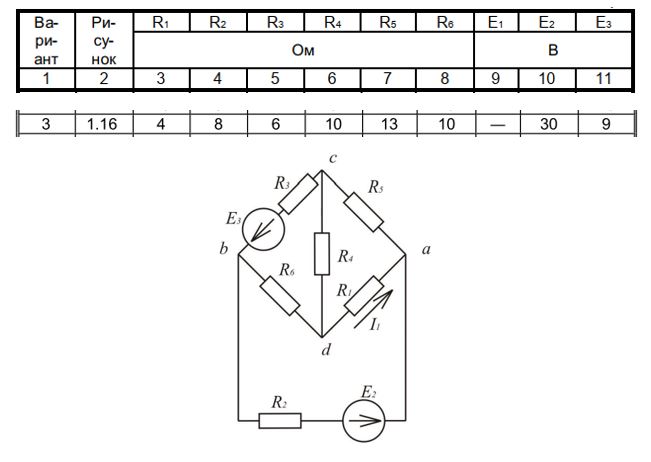
Вариант 3 (Схема 1.16)
Описание:
Подробное решение в WORD+файл MathCad
Поисковые тэги: Законы Кирхгофа, Метод контурных токов (МКТ), Метод эквивалентного генератора (МЭГ), Баланс мощностей, Потенциальная диаграмма, Метод узловых потенциалов (напряжений; МУП)
Изображение предварительного просмотра:
Процесс покупки очень прост и состоит всего из пары действий:
1. После нажатия кнопки «Купить» вы перейдете на сайт платежной системы, где можете выбрать наиболее удобный для вас способ оплаты (банковские карты, электронные деньги, с баланса мобильного телефона, через банкоматы, терминалы, в салонах сотовой связи и множество других способов)
2. После успешной оплаты нажмите ссылку «Вернуться в магазин» и вы снова окажетесь на странице описания задачи, где вместо зеленой кнопки «Купить» будет синяя кнопка «Скачать»
3. Если вы оплатили, но по каким-то причинам не смогли скачать заказ (например, случайно закрылось окно), то просто сообщите нам на почту или в чате артикул задачи, способ и время оплаты и мы отправим вам файл. Условия доставки: Получение файла осуществляется самостоятельно по ссылке, которая генерируется после оплаты. В случае технических сбоев или ошибок можно обратиться к администраторам в чате или на электронную почту и файл будет вам отправлен. Условия отказа от заказа: Отказаться возможно в случае несоответсвия полученного файла его описанию на странице заказа. Возврат денежных средств осуществляется администраторами сайта по заявке в чате или на электронной почте в течении суток.
