Артикул: 1165632
Раздел:Технические дисциплины (109134 шт.) >Теоретические основы электротехники (ТОЭ) (23595 шт.) >
Цепи переменного синусоидального тока (6338 шт.)
Название или условие:
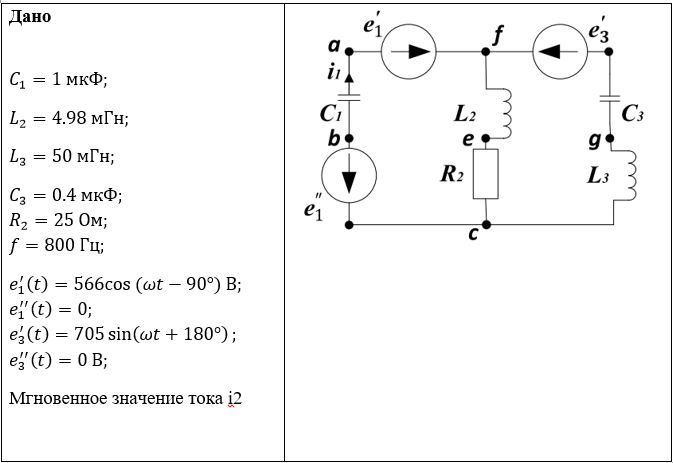
Для электрической схемы, соответствующей номеру варианта (табл. 1.3 ) и изображенной на рис 21-40 выполнить следующее:
1. На основании законов Кирхгофа составить в общем виде систему уравнений для расчета токов во всех ветвях цепи, записав ее в двух формах: а) дифференциальной; б) символической.
2. Определить комплексы действующих значений токов во всех ветвях, воспользовавшись одним из методов расчета линейных электрических цепей.
При выполнении п.2 учесть , что одна из ЭДС в табл. 2 может быть задана косинусоидой (не синусоидой). Чтобы правильно записать ее в виде комплексного числа, сначала надо от косинусоиды перейти к синусоиде.
3. Построить:
3.1. Векторную диаграмму токов на комплексной плоскости.
3.2. Топографическую диаграмму потенциалов точек электрической цепи.
Потенциал точки a, указанной на схеме, принять равным нулю.
4. Используя данные расчетов, полученных в п 2, записать выражение мгновенного значения тока или напряжения. Нарисовать график.
5. Полагая, что между двумя любыми индуктивными катушками, расположенными в различных ветвях заданной схемы, имеется магнитная связь при взаимной индуктивности, равной М, составить в общем виде систему уравнений по законам Кирхгофа для расчета токов во всех ветвях схемы, записав ее в двух формах: а) дифференциальной, б) символической
Описание:
Ориентируясь на ранее принятые направления токов в ветвях, одноименные зажимы индуктивных катушек выбрать так, чтобы их включение было встречное, и обозначить их на схеме точками.
В случае отсутствия в заданной схеме второй индуктивности, вторую катушку ввести дополнительно в одну из ветвей, не содержащих L.
Вариант 19
Подробное решение в WORD+файл MathCad
Поисковые тэги: Законы Кирхгофа, Векторная (топографическая) диаграмма, Индуктивная связь (магнитно-связанные катушки)
Изображение предварительного просмотра:
Процесс покупки очень прост и состоит всего из пары действий:
1. После нажатия кнопки «Купить» вы перейдете на сайт платежной системы, где можете выбрать наиболее удобный для вас способ оплаты (банковские карты, электронные деньги, с баланса мобильного телефона, через банкоматы, терминалы, в салонах сотовой связи и множество других способов)
2. После успешной оплаты нажмите ссылку «Вернуться в магазин» и вы снова окажетесь на странице описания задачи, где вместо зеленой кнопки «Купить» будет синяя кнопка «Скачать»
3. Если вы оплатили, но по каким-то причинам не смогли скачать заказ (например, случайно закрылось окно), то просто сообщите нам на почту или в чате артикул задачи, способ и время оплаты и мы отправим вам файл. Условия доставки: Получение файла осуществляется самостоятельно по ссылке, которая генерируется после оплаты. В случае технических сбоев или ошибок можно обратиться к администраторам в чате или на электронную почту и файл будет вам отправлен. Условия отказа от заказа: Отказаться возможно в случае несоответсвия полученного файла его описанию на странице заказа. Возврат денежных средств осуществляется администраторами сайта по заявке в чате или на электронной почте в течении суток.
