Артикул: 1165474
Раздел:Технические дисциплины (108973 шт.) >Теоретические основы электротехники (ТОЭ) (23510 шт.) >
Цепи переменного синусоидального тока (6325 шт.)
Название или условие:
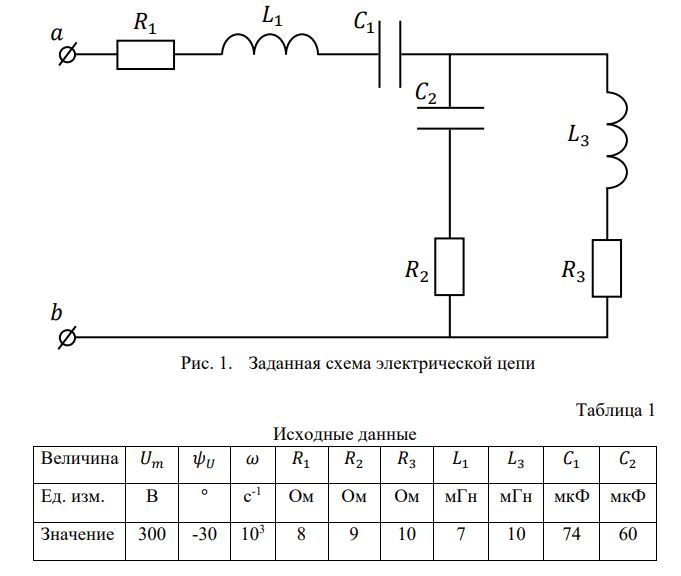
Расчёт цепи синусоидального тока (Курсовая работа)
Вариант №5.2
Описание:
Задание:
Исследуемая цепь изображена на рис. 1. Для цепи заданы все параметры
R, L и C, угловая частота ω, амплитуда Um и начальная фаза Ψu
приложенного синусоидального напряжения (см. Таблица 1)
Требуется:
1. Написать выражения для приложенного мгновенного напряжения и
изображающих его комплексной амплитуды напряжения и
комплекса действующего значения напряжения.
2. Определить во всех ветвях цепи:
a) комплексные амплитуды токов и комплексы действующих
значений токов;
b) мгновенные значения токов.
3. Построить в одной комплексной плоскости векторную диаграмму
токов и топографическую диаграмму напряжений ветвей и всей
цепи.
4. Определить активные, реактивные и комплексные мощности всех
ветвей и цепи в целом. Составить баланс мощностей.
5. Исследуемую цепь представить в виде пассивного двухполюсника.
Для двухполюсника:
a) ток I и напряжение U на его входе разложить графически и
аналитически на активные и реактивные составляющие;
b) определить угол сдвига фаз φ между током I и напряжением
U на его входе; написать, который из этих векторов является
опережающим;
c) определить входное комплексное сопротивление Z и
составить соответствующую схему двухполюсника с
последовательным соединением сопротивлений R и jX;
d) определить входную комплексную проводимость Y и
составить соответствующую ей схему двухполюсника с
параллельным соединением проводимостей g и jb.
6. Для первой ветви (приняв сопротивление остальных ветвей
равными нулю):
a) составить выражения для мгновенных напряжений и
мощностей всей ветви и на каждом ее элементе (u1, uR, uL, uC, p1, pR, pL, pC, pр);
b) составить выражения для мгновенной энергии магнитного
поля индуктивности wL и электрического поля емкости wC;
c) построить графики мгновенного напряжения, мгновенного
тока и всех величин, перечисленных в пунктах а) и b) в
функции времени.
Подробное решение в PDF - 17 страниц
Поисковые тэги: Баланс мощностей, Векторная (топографическая) диаграмма
Изображение предварительного просмотра:
Процесс покупки очень прост и состоит всего из пары действий:
1. После нажатия кнопки «Купить» вы перейдете на сайт платежной системы, где можете выбрать наиболее удобный для вас способ оплаты (банковские карты, электронные деньги, с баланса мобильного телефона, через банкоматы, терминалы, в салонах сотовой связи и множество других способов)
2. После успешной оплаты нажмите ссылку «Вернуться в магазин» и вы снова окажетесь на странице описания задачи, где вместо зеленой кнопки «Купить» будет синяя кнопка «Скачать»
3. Если вы оплатили, но по каким-то причинам не смогли скачать заказ (например, случайно закрылось окно), то просто сообщите нам на почту или в чате артикул задачи, способ и время оплаты и мы отправим вам файл. Условия доставки: Получение файла осуществляется самостоятельно по ссылке, которая генерируется после оплаты. В случае технических сбоев или ошибок можно обратиться к администраторам в чате или на электронную почту и файл будет вам отправлен. Условия отказа от заказа: Отказаться возможно в случае несоответсвия полученного файла его описанию на странице заказа. Возврат денежных средств осуществляется администраторами сайта по заявке в чате или на электронной почте в течении суток.
