Артикул: 1151813
Раздел:Технические дисциплины (97023 шт.) >Математика (32680 шт.) >
Линейная алгебра (1788 шт.)
Название или условие:
Решите неравенство
Описание:
Подробное решение
Изображение предварительного просмотра:
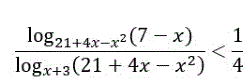
Процесс покупки очень прост и состоит всего из пары действий:
1. После нажатия кнопки «Купить» вы перейдете на сайт платежной системы, где можете выбрать наиболее удобный для вас способ оплаты (банковские карты, электронные деньги, с баланса мобильного телефона, через банкоматы, терминалы, в салонах сотовой связи и множество других способов)
2. После успешной оплаты нажмите ссылку «Вернуться в магазин» и вы снова окажетесь на странице описания задачи, где вместо зеленой кнопки «Купить» будет синяя кнопка «Скачать»
3. Если вы оплатили, но по каким-то причинам не смогли скачать заказ (например, случайно закрылось окно), то просто сообщите нам на почту или в чате артикул задачи, способ и время оплаты и мы отправим вам файл. Условия доставки: Получение файла осуществляется самостоятельно по ссылке, которая генерируется после оплаты. В случае технических сбоев или ошибок можно обратиться к администраторам в чате или на электронную почту и файл будет вам отправлен. Условия отказа от заказа: Отказаться возможно в случае несоответсвия полученного файла его описанию на странице заказа. Возврат денежных средств осуществляется администраторами сайта по заявке в чате или на электронной почте в течении суток.
