Артикул: 1151436
Раздел:Технические дисциплины (96654 шт.) >Теоретические основы электротехники (ТОЭ) (13801 шт.)
Название или условие:
Анализ сложных электрических цепей в установившемся и переходном режимах (Курсовая работа)
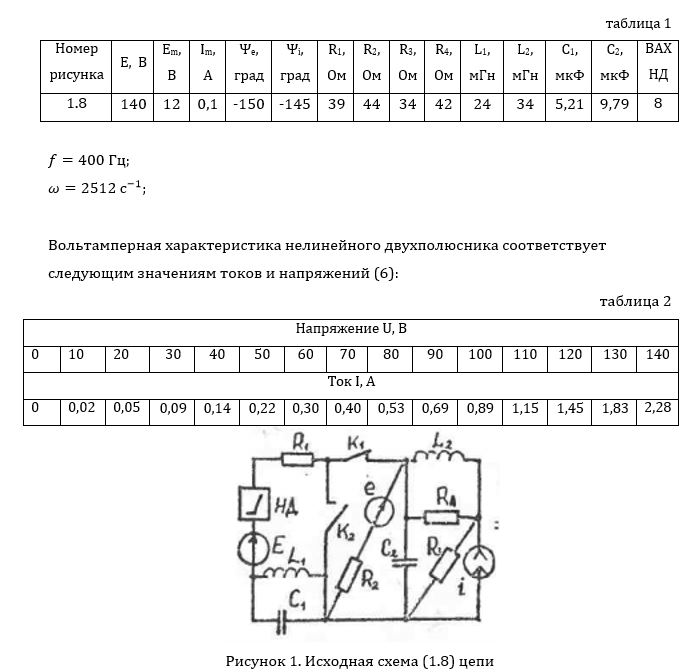
Исследовать электрическую цепь с нелинейным резистивным двухполюсником, в которой действуют источник ЭДС Е и источники однофазной синусоидальной ЭДС e=Emsin(ωt+ψu) и однофазного синусоидального тока i=Imsin(ωt+ψi) с частотой f=400 Гц.
Вариант 8
Описание:
Задание 1. Расчет установившегося режима.
1.1.Рассчитать установившийся режим в линеаризованной цепи на постоянном токе, с этой целью:
1.1.1. Провести линеаризацию ВАХ НД двухполюсника с помощью секущей.
1.1.2. Построить схему линеаризованной цепи на постоянном токе.
1.1.3. Рассчитать токи в ветвях и напряжения на элементах. Проверить правильность расчета, составив баланс мощностей.
1.2.Рассчитать установившийся режим в линеаризованной цепи на переменном токе, с этой целью:
1.2.1. Построить схему линеаризованной цепи на переменном токе.
1.2.2. Записать уравнения для цепи в комплексной форме по методам контурных
токов и узловых напряжений (с подставленными числовыми данными).
1.2.3. Определить на ЭВМ токи в ветвях и напряжения на пассивных
элементах, проверить правильность расчета составлением баланса мощностей.
1.3. Сформулировать установившийся режим в линеаризованной цепи с учетом всех источников энергий, с этой целью:
1.3.1. Записать в мгновенной форме токи в ветвях и напряжения на
элементах линеаризованной цепи с учетом всех источников энергии.
1.3.2. Построить графики изменения мгновенных значений тока и напряжения в линеаризованной цепи для НД и одного из реактивных элементов.
Задание 2. Расчет переходного режима.
2.1. Учитывая, что в результате коммутации схема заданной электрической цепи разделяется на две независимых части, рассчитать переходный процесс в части схемы с источником постоянной ЭДС при линеаризации нелинейного двухполюсника, для этого:
2.1.1. Построить схему для исследуемой части электрической цепи.
2.1.2. Из расчета установившегося режима в заданной цепи определить независимые начальные условия.
2.1.3. Рассчитать начальные значения остальных токов и напряжений в схеме исследуемой части электрической цепи.
2.1.4. Вычислить искомую функцию тока или напряжения
2.1.5. Дать характеристику переходного процесса и определить его длительность.
2.1.6. Проверить правильность расчета переходного процесса на ЭВМ
2.1.1. По результатам расчетов, выполненных на ЭВМ и вручную, построить график искомой функции до коммутации (в пределах периода установившегося режима) и после коммутации (в пределах длительности переходного процесса).
2.1.8. Сравнить результаты расчета переходного процесса в схеме, полученные на компьютере и вручную.
2.2. Рассчитать переходный процесс в части заданной схемы с источниками синусоидального ЭДС и тока, для этого:
2.2.1. Построить схему для исследуемой части электрической цепи
2.2.2. Из расчета установившегося режима в цепи определить независимые начальные условия
2.2.3. Рассчитать начальные значения остальных токов и напряжений в схеме цепи
2.2.4. Дать характеристику переходного процесса в цепи и определить его длительность
2.2.5. На ЭВМ вычислить искомую функцию тока или напряжения
2.2.6. По результатам расчета построить график искомой функции до и после коммутации (аналогично п.2.1).
Задание 3. Расчет установившегося режима в исходной нелинейной цепи
3.1. Учитывая, что для заданной цепи выполняются условия E>>Em, E>>ImZвт(i), где Zвт(i) – внутреннее сопротивление источника тока, рассчитать установившийся режим в нелинеаризованной цепи на постоянном токе, с этой целью:
3.1.1. Построить схему нелинейной цепи на постоянном токе.
3.1.2. Определить на ВАХ НД положение рабочей точки
3.1.3. Рассчитать токи в ветвях и напряжения на пассивных элементах цепи с учетом найденных параметров рабочей точки, составить баланс мощностей.
3.1.4. Определить статическое и дифференциальное сопротивление НД в рабочей точке.
Подробное решение в WORD (22 страницы)+файл MathCad+файл моделирования Microcap
Поисковые тэги: Баланс мощностей, Классический метод, MicroCap
Изображение предварительного просмотра:
Процесс покупки очень прост и состоит всего из пары действий:
1. После нажатия кнопки «Купить» вы перейдете на сайт платежной системы, где можете выбрать наиболее удобный для вас способ оплаты (банковские карты, электронные деньги, с баланса мобильного телефона, через банкоматы, терминалы, в салонах сотовой связи и множество других способов)
2. После успешной оплаты нажмите ссылку «Вернуться в магазин» и вы снова окажетесь на странице описания задачи, где вместо зеленой кнопки «Купить» будет синяя кнопка «Скачать»
3. Если вы оплатили, но по каким-то причинам не смогли скачать заказ (например, случайно закрылось окно), то просто сообщите нам на почту или в чате артикул задачи, способ и время оплаты и мы отправим вам файл. Условия доставки: Получение файла осуществляется самостоятельно по ссылке, которая генерируется после оплаты. В случае технических сбоев или ошибок можно обратиться к администраторам в чате или на электронную почту и файл будет вам отправлен. Условия отказа от заказа: Отказаться возможно в случае несоответсвия полученного файла его описанию на странице заказа. Возврат денежных средств осуществляется администраторами сайта по заявке в чате или на электронной почте в течении суток.
