Артикул: 1132128

Раздел:Технические дисциплины (81430 шт.) >
  Математика (30920 шт.) >
  Численные методы и вычислительная математика (392 шт.)

Название или условие:
Лабораторная работа № 4
Решение типовых задач о кривых второго порядка на плоскости в системе MATLAB
Вариант 3

Описание:
Задача 1.
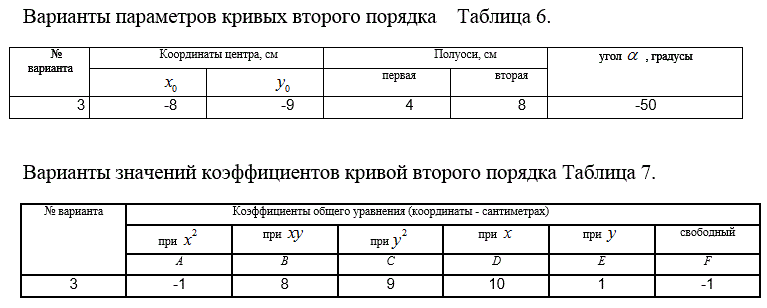
В табл.6 даны координаты центра эллипса и гиперболы, а также величины их полуосей. Первая полуось повёрнута против часовой стрелки относительно горизонтальной координатной оси на угол α.
В поле axes фигуры MATLAB построить эллипс и гиперболу с заданным центром, полуосями и углом поворота. Первая ось гиперболы - действительная, вторая - мнимая. Построить параболу, проходящую через точку с фокусным расстоянием, равным первой полуоси, причём ось параболы совпадает с первой осью эллипса и гиперболы. При построении применить уравнения кривых в параметрической форме.

Задача 2.
Кривая второго порядка задана общим уравнением
A·x²+B·x·y+C·y²+D·x+E·y+F=0
Коэффициенты А, В, С, D, Е, F представлены в табл.7.

Определить центр, направление осей, полуоси (в случае параболы - фокусное расстояние). Построить заданную кривую, пользуясь параметрическим уравнением, по 513 точкам. Если получился эллипс, то построить его главные оси. Если получилась гипербола, то построить её асимптоты, отметить точку их пересечения маркером в виде кружочка. Если полуоси получились конечными, то убедиться, что координаты всех рассчитанных точек кривой удовлетворяют исходному уравнению.

Подробное решение в WORD+исходники MatLab

Поисковые тэги: MatLab

Изображение предварительного просмотра:

Процесс покупки очень прост и состоит всего из пары действий:
1. После нажатия кнопки «Купить» вы перейдете на сайт платежной системы, где можете выбрать наиболее удобный для вас способ оплаты (банковские карты, электронные деньги, с баланса мобильного телефона, через банкоматы, терминалы, в салонах сотовой связи и множество других способов)
2. После успешной оплаты нажмите ссылку «Вернуться в магазин» и вы снова окажетесь на странице описания задачи, где вместо зеленой кнопки «Купить» будет синяя кнопка «Скачать»
3. Если вы оплатили, но по каким-то причинам не смогли скачать заказ (например, случайно закрылось окно), то просто сообщите нам на почту или в чате артикул задачи, способ и время оплаты и мы отправим вам файл.
Условия доставки:
Получение файла осуществляется самостоятельно по ссылке, которая генерируется после оплаты. В случае технических сбоев или ошибок мозно обратиться к администраторам в чате или на электронную почту и файл будет вам отправлен.
Условия отказа от заказа:
Отказаться возможно в случае несоответсвия поулченного файла его описанию на странице заказа.
Возврат денежных средств осуществляется администраторами сайта по заявке в чате или на электронной почте в течении суток.

Похожие задания:

Многомерная оптимизация Методом Ньютона найти с точностью ε=10-4 минимум функции Вариант 3	Интерполяция-1 Используя интерполяционный многочлен Лагранжа, приблизить функцию, заданную таблично. Вычислить приближенное значение в точке x0 (вычисление вести с четырьмя знаками после запятой). Вариант 1
Решение систем линейных алгебраических уравнений Решить систему линейных алгебраических уравнений Ах=В а) методом Гаусса с выбором главного элемента б) методом простых итераций (с оценкой достаточного числа итераций) в) методом Зайделя Решение найти с точностью 10-3 В промежуточных вычислениях удерживать 4-5 знаков после запятой Вариант 9	Численное интегрирование Вычислить интеграл от многочлена P(x) в пределах от 1 до 2.2 с шагом h = 0.2, используя формулы: а) центральных прямоугольников; б) трапеций; в) Симпсона. Оценить погрешность результатов. Проверить справедливость оценок, сравнив полученные приближенные значения интеграла с точным значением, вычисленным по формуле Ньютона-Лейбница Значение многочлена вычислять по схеме Горнера. Промежуточные вычисления вести с шестью значащими цифрами. Ответы записать с учетом погрешности Вариант 10
Многомерная оптимизация Методом Ньютона найти с точностью ε=10-4 минимум функции Вариант 1	Задача Коши Численно решить задачу Коши для обыкновенного дифференциального уравнения 1-го порядка на отрезке [a,b] с шагом h=0.2, h=0.4 а) методом Эйлера б) исправленным методом Эйлера в) методом Эйлера-Коши Оценить погрешность по правилу Рунге. Найти точное решение задачи. Убедиться в правильности полученной оценки. Построить графики точного и приближенного решений Вариант 3
Решение систем линейных алгебраических уравнений Решить систему линейных алгебраических уравнений Ах=В а) методом Гаусса с выбором главного элемента б) методом простых итераций (с оценкой достаточного числа итераций) в) методом Зайделя Решение найти с точностью 10-3 В промежуточных вычислениях удерживать 4-5 знаков после запятой Вариант 10	Многомерная оптимизация Методом Ньютона найти с точностью ε=10-4 минимум функции Вариант 5
Метод наименьших квадратов Применяя метод наименьших квадратов, приблизить функцию, заданную таблично, ее многочленами 1-ой и 2-ой степени. Для каждого приближения определить величину среднеквадратичной погрешности, построить график Вариант 10	Одномерная оптимизация Методом золотого сечения найти с точностью ε=10-1 минимум функции. Выбрав полученное решение в качестве начального приближения, найти решение уравнения методом бисекции с точностью ε=10-3 и Ньютона с точностью ε = 10-4 Вариант 3