Артикул: 1070744

Раздел:Технические дисциплины (57837 шт.) >
  Теоретическая механика (теормех, термех) (1461 шт.) >
  Динамика (237 шт.)

Название или условие:
Динамическое исследование движения системы с одной степенью свободы (Вариант 211)

Описание:
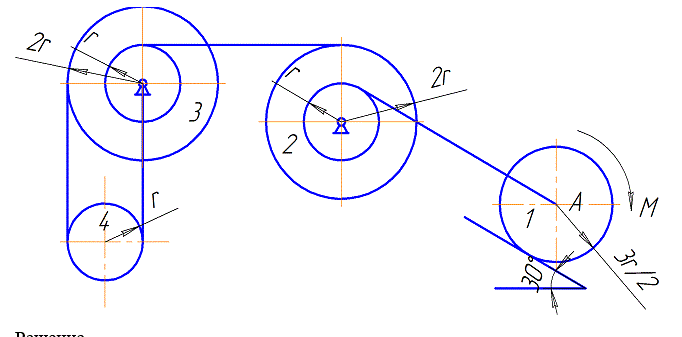
Механическая система состоит из четырех цилиндров, связанных между собой нерастяжимыми тросами. Каток 1 массы m₁=4∙m mрадиуса r₁=(3r/2)r катится без скольжения по неподвижной плоскости, наклоненной под углом α = 30° к горизонту. Блоки 2 и 3 – одинаковые сплошные однородные сдвоенные цилиндры массы m₂=m₃=20∙m с внутренним радиусом r₂=r₃=r и наружным радиусом R₂=R₃=2r. Даны радиусы инерции цилиндров
ρ₂²=ρ₃²=(3r²)/2
Величины m и r считаются заданными.
Система приводится в движение из состояния покоя моментом
M=M₀∙((t+2)/(t+1))
приложенным к катку 1.
1. Используя общие теоремы динамики, составить систему уравнений, описывающих движение заданной механической системы. Исключая из этой системы уравнений внутренние силы, получить дифференциальное уравнение, служащее для определения зависимости s(t) координаты точки А от времени - дифференциальное уравнение движения системы.
2. Получить то же самое дифференциальное уравнение движения системы, используя теорему об изменении кинетической энергии в
дифференциальной форме.
3. Получить дифференциальное уравнение движения механической системы на основании общего уравнения динамики.
4. Убедившись в совпадении результатов, полученных четырьмя
независимыми способами, проинтегрировать дифференциальное уравнение движения системы, получив зависимость s(t) координаты точки А от времени.
5. Определить натяжения тросов в начальный момент времени (при t = 0).

Подробное решение в WORD - 9 страниц

Изображение предварительного просмотра:

Процесс покупки очень прост и состоит всего из пары действий:
1. После нажатия кнопки «Купить» вы перейдете на сайт платежной системы, где можете выбрать наиболее удобный для вас способ оплаты (банковские карты, электронные деньги, с баланса мобильного телефона, через банкоматы, терминалы, в салонах сотовой связи и множество других способов)
2. После успешной оплаты нажмите ссылку «Вернуться в магазин» и вы снова окажетесь на странице описания задачи, где вместо зеленой кнопки «Купить» будет синяя кнопка «Скачать»
3. Если вы оплатили, но по каким-то причинам не смогли скачать заказ (например, случайно закрылось окно), то просто сообщите нам на почту или в чате артикул задачи, способ и время оплаты и мы отправим вам файл.
Условия доставки:
Получение файла осуществляется самостоятельно по ссылке, которая генерируется после оплаты. В случае технических сбоев или ошибок мозно обратиться к администраторам в чате или на электронную почту и файл будет вам отправлен.
Условия отказа от заказа:
Отказаться возможно в случае несоответсвия поулченного файла его описанию на странице заказа.
Возврат денежных средств осуществляется администраторами сайта по заявке в чате или на электронной почте в течении суток.

Похожие задания:

Задача 3.2 Вертикальный вал АВ (рис.1.2), вращающийся с постоянной угловой скоростью ω, закреплен подпятником в точке А и цилиндрическим подшипником в точке В К валу жестко прикреплен невесомый стержень длиной l с точечной массой m на конце. Пренебрегая весом вала, определить реакции подпятника А и подшипника В. Вариант 5 Дано: ω=10c-1-const, l=0.4м, a=b=0.6м, m=2кг, α=60°, g≈10м/c2. Определить: YA, ZA, RB-?	Лыжник массой m = 70 кг опускается без начальной скорости по склону, составляющему угол α = 30° с горизонтом, не отталкиваясь палками. Длина спуска l = 100 м, коэффициент трения скольжения лыж о снег f = 0.1. Сила сопротивления воздуха пропорциональна квадрату скорости R = 0.4v2. Определить скорость лыжника в конце спуска.
Груз D массой m, получив в точке А начальную скорость V0, движется в изогнутой трубе ABC, расположенной в вертикальной плоскости; участки трубы один горизонтальный, другой вертикальный. На участке АВ на груз кроме силы тяжести действуют постоянная сила Q (ее направление показано на рис.1.1) и сила сопротивления среды R, зависящая от скорости V груза (направлена против движения), трением груза о трубу на участке АВ пренебречь. В точке В груз, не изменяя своей скорости, переходит на участок ВС трубы, где на него кроме силы тяжести действуют сила трения (коэффициент трения груза о трубу f) и переменная сила F, проекция которой F_x на ось Bх задана. Считая груз материальной точкой и зная время t1 движения груза от точки А до точки В, найти закон движения груза на участке ВС. Вариант 3.6	Практическое задание 5 «Движение материальной точки под действием постоянных сил» Вариант 54(24). Варианты 21…25 (схема 5). Тело движется из точки А по участку АВ (длиной l) наклонной плоскости, составляющей угол α с горизонтом. Его начальная скорость VA. Коэффициент трения скольжения равен f. Через τ секунд тело в точке В со скоростью VB покидает наклонную плоскость и падает на горизонтальную плоскость в точку С со скоростью VC при этом оно находится в воздухе Т секунд. При решении задачи принять тело за материальную точку и не учитывать сопротивление воздуха. Дано: VA=0, d=12м, l=10м, α=30°, f=0.2. Определить: τ, h-?
Найдите ускорение тела (1)	Определить: 1. главный вектор сил инерции блока 2; 2. главный момент сил инерции блока 2; 3. натяжение нити между грузом и блоком; 4. массу груза 1; 5. минимальную массу груза 1, при которой система будет находиться в покое. Вариант 22
Задание Д.10. Применение теоремы об изменении кинетической энергии к изучению движения механической системы Механическая система под действием сил тяжести приходит в движение из состояния покоя. Начальное положение системы показано на рис. 1. Учитывая сопротивление качению тела 3, катящегося без скольжения, пренебрегая другими силами сопротивления и массами нитей, предполагаемых нерастяжимыми, определить скорость тела 1 в тот момент, когда пройденный им путь станет равным s. Блоки в катки, для которых радиусы инерции в таблице не указаны, считать сплошными однородными цилиндрами. Наклонные участки нитей параллельны соответствующим наклонным плоскостям. Вариант 7 Дано: m1 = m; m2 = 2m; m3 = 2m; R2 = 16 см; R3 = 25 см; i2х = 14 см; α = 30°; δ = 0,20; s = 2 м.	Задача Д1 Динамика материальной точки Груз D массой m, получив в точке А начальную скорость, движется в изогнутой трубе АВС, расположенной в вертикальной плоскости. На участке АВ на груз кроме силы тяжести действует постоянная сила Q=10Н, направленная от точки А к точке В, и сила сопротивления среды R , зависящая от скорости V груза D: R=μVn. В точке В груз, изменив направление приобретенной скорости, но, сохранив при этом ее величину, переходит на участок ВС трубы, где на него, помимо силы тяжести действует сила трения (коэффициент трения груза о трубу f=0,2) и переменная по величине сила F=F(t), направленная вдоль участка ВС. Проекция Fx последней на ось Вх задается. Считая груз D материальной точкой, и зная расстояние АВ или время t движения груза от точки А до точки В, найти уравнение х=х(t) движения груза на участке ВС. Вариант 11-5
Индивидуальное задание №3 Вариант №28 Механическая система, состоящая из абсолютно твердых тел, под действием сил тяжести приходит в движение из состояния покоя с недеформированной невесомой пружиной; начальное положение системы показано на рисунке 1. Учитывая упругую силу в момент сопротивления качению, определить скорость v1 тела 1 в тот момент, когда пройденный им путь станет равным S1. Другими силами сопротивления пренебречь.	Практическое задание 7 «Общее уравнение динамики» Номер варианта задается преподавателем и соответствует номеру на рисунке. Для заданной механической системы определить ускорение груза. Массами нитей пренебречь. Трение качения и силы сопротивления в подшипниках не учитывать. Система движется из состояния покоя. Варианты механических систем показаны на рисунке, необходимые для решения данные приведены в таблице. Блоки и катки, для которых радиусы инерции в таблице указаны, считать сплошными однородными цилиндрами. Вариант 20 (Схема 20) Дано: G1=4*G, G2=0.2*G, G3=0.1*G, G4=3*G, R2=1.8*r, r2=1.5*r, i2=1.6*r, i3=r*√2, R3=2*r, r3=r, g≈10м/с2. Найти: a1, T1-?